Sztuczne sieci neuronowe (ANN ): Różnice pomiędzy wersjami
| (Nie pokazano 67 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 2: | Linia 2: | ||
[[Wnioskowanie_Statystyczne_-_wykład]] | [[Wnioskowanie_Statystyczne_-_wykład]] | ||
| − | = | + | =Uczenie (maszynowe, ML) nadzorowane (supervised learning)= |
| − | [[Plik:The-linear-borders-between-the-groups-for-LR-solid-and-LDA-dotted-line.png|right|thumb|frame|linie podziału z LDA i LR, z pracy "Comparison of Logistic Regression and Linear Discriminant Analysis: A Simulation Study", M. Pohar, M. Blas, and S. Turk, ''Metodološki zvezki'', Vol. 1, No. 1, 2004, 143-161]] | + | Dane mamy podzielone na grupy, |
| + | szukamy funkcji najlepiej je rozdzielającej, która umożliwi | ||
| + | zaklasyfikowanie nowej obserwacji do jednej z tych grup. | ||
| + | |||
| + | '''Zdefiniowany powyżej cel jest zasadniczo różny od jak najdokładniejszej estymacji p-wartości, która była przedmiotem większości dotychczasowych rozważań.''' | ||
| + | |||
| + | |||
| + | |||
| + | ==Regresja Logistyczna (''Logistic regression, LR'')== | ||
| + | <!-- [[Plik:The-linear-borders-between-the-groups-for-LR-solid-and-LDA-dotted-line.png|right|thumb|frame|linie podziału z LDA i LR, z pracy "Comparison of Logistic Regression and Linear Discriminant Analysis: A Simulation Study", M. Pohar, M. Blas, and S. Turk, ''Metodološki zvezki'', Vol. 1, No. 1, 2004, 143-161]] --> | ||
| + | |||
| + | Omawiana wcześniej [[WnioskowanieStatystyczne/Regresja_liniowa|regresja liniowa]] opierała się na linowej zależności między zmienną niezależną <math>x</math> a zmienną zależną <math>y</math> | ||
| + | :<math>y = a x + b</math> | ||
| + | |||
| + | Regresję logistyczną stosujemy w przypadku, gdy zmienna zależna jest jakościowa (wyliczeniowa / czynnikowa / kategoryczna = ''categorical variable''). Nie szacujemy wtedy wartości <math>y</math> na podstawie <math>x</math>, tylko prawdopodobieństwo przynależności <math>x</math> do jednej z klas (kategorii) <math>K_i</math>. | ||
| + | :<math>P(K_i | x) = \frac{1}{1 - e^ {-(a x + b)}}</math> | ||
| + | [[Plik:Lin_log_reg.png|center|frameless|600px]] | ||
| + | |||
| + | Podobnie jak w przypadku regresji liniowej, parametry <math>a</math> i <math>b</math> możemy estymować [[WnioskowanieStatystyczne/MLF | metodą największej wiarygodności]]. Niestety w przypadku LR nie daje się znaleźć rozwiązania analitycznego, do maksymalizacji prawdopodobieństwa a posteriori stosowane są zwykle metody gradientowe. | ||
| + | |||
| + | |||
| + | |||
| + | ==Liniowa Analiza dyskryminacyjna (''Linear Discriminant Analysis, LDA'')== | ||
| + | Do każdego punktu danych (potencjalnie wielowymiarowych) mamy przypisaną przynależność do jednej z 2 (w klasycznym podejściu Fischera z 1936r.) lub więcej grup/klas. Założenia o danych wejściowych: rozkład normalny, [https://pl.wikipedia.org/wiki/Homoskedastyczno%C5%9B%C4%87 homoskedastyczność], niezależność. | ||
| + | Wykorzystywana jest do znalezienia liniowej kombinacji cech, które najlepiej rozróżniają klasy. | ||
| + | |||
| + | ''[https://en.wikipedia.org/wiki/Linear_discriminant_analysis In bankruptcy prediction based on accounting ratios and other financial variables, linear discriminant analysis was the first statistical method applied to systematically explain which firms entered bankruptcy vs. survived. Despite limitations including known nonconformance of accounting ratios to the normal distribution assumptions of LDA, Edward Altman's 1968 model is still a leading model in practical applications.]'' | ||
| + | |||
| + | Na LDA opierały się też w dużej części techniki psychologicznego mikrotargetowania opracowane przez [https://pl.wikipedia.org/wiki/Micha%C5%82_Kosi%C5%84ski Michała Kosińskiego], użytego pomimo jego ostrzeżeń (por. artykuł [https://www.pnas.org/doi/10.1073/pnas.1710966114 "Psychological targeting as an effective approach to digital mass persuasion"]) przez [https://en.wikipedia.org/wiki/Cambridge_Analytica Cambridge Analitica]. | ||
| + | |||
| + | ===Przykład: gatunki Kosaćca ([https://en.wikipedia.org/wiki/Iris_flower_data_set Iris flower dataset])=== | ||
| + | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| + | | <strong>dane </strong> | ||
| + | |- | ||
| + | | <pre> | ||
| + | s_length s_width p_length p_width species | ||
| + | 0 5.1 3.5 1.4 0.2 0 | ||
| + | 1 4.9 3.0 1.4 0.2 0 | ||
| + | 2 4.7 3.2 1.3 0.2 0 | ||
| + | 3 4.6 3.1 1.5 0.2 0 | ||
| + | 4 5.0 3.6 1.4 0.2 0 | ||
| + | .. ... ... ... ... ... | ||
| + | 145 6.7 3.0 5.2 2.3 2 | ||
| + | 146 6.3 2.5 5.0 1.9 2 | ||
| + | 147 6.5 3.0 5.2 2.0 2 | ||
| + | 148 6.2 3.4 5.4 2.3 2 | ||
| + | 149 5.9 3.0 5.1 1.8 2 | ||
| + | [150 rows x 5 columns] | ||
| + | </pre> | ||
| + | |} | ||
| + | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| + | | <strong>macierz kowariancji </strong> | ||
| + | |- | ||
| + | | <pre> | ||
| + | s_length s_width p_length p_width | ||
| + | s_length 0.685694 -0.042434 1.274315 0.516271 | ||
| + | s_width -0.042434 0.189979 -0.329656 -0.121639 | ||
| + | p_length 1.274315 -0.329656 3.116278 1.295609 | ||
| + | p_width 0.516271 -0.121639 1.295609 0.581006 | ||
| + | </pre> | ||
| + | |} | ||
| + | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| + | | <strong>macierz korelacji </strong> | ||
| + | |- | ||
| + | | <pre> | ||
| + | s_length s_width p_length p_width | ||
| + | s_length 1.000000 -0.117570 0.871754 0.817941 | ||
| + | s_width -0.117570 1.000000 -0.428440 -0.366126 | ||
| + | p_length 0.871754 -0.428440 1.000000 0.962865 | ||
| + | p_width 0.817941 -0.366126 0.962865 1.000000 | ||
| + | </pre> | ||
| + | |} | ||
| + | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| + | | <strong>kod </strong> | ||
| + | |- | ||
| + | | <pre> | ||
| + | #sepal --- działki kielicha | ||
| + | #Iris --- Kosaciec | ||
| + | import pandas as pd | ||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | import seaborn | ||
| + | from sklearn import datasets | ||
| + | iris=datasets.load_iris() | ||
| + | # convert dataset into a pandas dataframe | ||
| + | df = pd.DataFrame(data = np.c_[iris['data']], columns = iris['feature_names']) | ||
| + | df['species'] = pd.Categorical.from_codes(iris.target, iris.target_names) | ||
| + | df.columns = ['s_length', 's_width', 'p_length', 'p_width','species'] | ||
| + | seaborn.pairplot(df, hue="species") #, diag_kind="hist") | ||
| + | plt.show() | ||
| + | |||
| + | df2 = df[df.columns[:-1]] | ||
| + | print('\nkowariancja:\n', df2.cov()) | ||
| + | print('\nkorelacja:\n', df2.corr()) | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | |||
| + | [[Plik:Kosaciec scatter.png|600px]] | ||
| + | |||
| + | ==Przykładowe wyniki zastosowania LDA, LR i modelu wyższego rzędu (QDA) do par cech.== | ||
| + | Docelowo klasyfikacje robimy oczywiście w oparciu o wszystkie cechy, ale w dwóch wymiarach łatwiej zaobserwować własności metod. | ||
| + | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| + | | <strong>kod</strong> | ||
| + | |- | ||
| + | | <pre> | ||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | from sklearn import datasets | ||
| + | from sklearn.discriminant_analysis import LinearDiscriminantAnalysis, QuadraticDiscriminantAnalysis | ||
| + | from sklearn.linear_model import LogisticRegression | ||
| + | from sklearn.preprocessing import StandardScaler | ||
| + | |||
| + | iris = datasets.load_iris() | ||
| + | # Bierzemy tylko dwie cechy dla wizualizacji: | ||
| + | # [:,:2] --- sepal | ||
| + | # [:,2:] --- petal | ||
| + | |||
| + | X = iris.data[:, 2:] | ||
| + | feature_names = iris.feature_names[2:] | ||
| + | target_names = iris.target_names | ||
| + | y = iris.target | ||
| + | X_scaled=X | ||
| + | # Inicjalizacja modeli | ||
| + | lda = LinearDiscriminantAnalysis() | ||
| + | logreg = LogisticRegression() | ||
| + | qda = QuadraticDiscriminantAnalysis() | ||
| + | # Trenowanie modeli | ||
| + | lda.fit(X_scaled, y) | ||
| + | logreg.fit(X_scaled, y) | ||
| + | qda.fit(X_scaled, y) | ||
| + | # Tworzenie siatki punktów dla wizualizacji | ||
| + | h = 0.02 # Rozmiar siatki | ||
| + | x_min, x_max = X_scaled[:, 0].min() - 1, X_scaled[:, 0].max() + 1 | ||
| + | y_min, y_max = X_scaled[:, 1].min() - 1, X_scaled[:, 1].max() + 1 | ||
| + | lda_grid_x, lda_grid_y = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) | ||
| + | logreg_grid_x, logreg_grid_y = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) | ||
| + | qda_grid_x, qda_grid_y = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) | ||
| + | lda_grid = np.c_[lda_grid_x.ravel(), lda_grid_y.ravel()] | ||
| + | logreg_grid = np.c_[logreg_grid_x.ravel(), logreg_grid_y.ravel()] | ||
| + | qda_grid = np.c_[qda_grid_x.ravel(), qda_grid_y.ravel()] | ||
| + | # Predykcja klas dla punktów na siatce w metodzie LDA | ||
| + | lda_pred_grid = lda.predict(lda_grid) | ||
| + | lda_pred_grid = lda_pred_grid.reshape(lda_grid_x.shape) | ||
| + | # Predykcja klas dla punktów na siatce w metodzie regresji logistycznej | ||
| + | logreg_pred_grid = logreg.predict(logreg_grid) | ||
| + | logreg_pred_grid = logreg_pred_grid.reshape(logreg_grid_x.shape) | ||
| + | # Predykcja klas dla punktów na siatce w metodzie QDA | ||
| + | qda_pred_grid = qda.predict(qda_grid) | ||
| + | qda_pred_grid = qda_pred_grid.reshape(qda_grid_x.shape) | ||
| + | |||
| + | # Wykresy | ||
| + | fig, axes = plt.subplots(1, 3, figsize=(15, 5)) | ||
| + | # Wykres dla LDA | ||
| + | ax1 = axes[0] | ||
| + | for color, i, target_name in zip(['navy', 'turquoise', 'darkorange'], [0, 1, 2], target_names): | ||
| + | ax1.scatter(X_scaled[y == i, 0], X_scaled[y == i, 1], color=color, alpha=0.8, lw=2, label=target_name) | ||
| + | ax1.contourf(lda_grid_x, lda_grid_y, lda_pred_grid, alpha=0.3, cmap='Set1') | ||
| + | ax1.set(xlim=(x_min, x_max), ylim=(y_min, y_max)) | ||
| + | ax1.set_title('LDA') | ||
| + | ax1.set_xlabel(feature_names[0]) | ||
| + | ax1.set_ylabel(feature_names[1]) | ||
| + | ax1.legend() | ||
| + | # Wykres dla regresji logistycznej | ||
| + | ax2 = axes[1] | ||
| + | for color, i, target_name in zip(['navy', 'turquoise', 'darkorange'], [0, 1, 2], target_names): | ||
| + | ax2.scatter(X_scaled[y == i, 0], X_scaled[y == i, 1], color=color, alpha=0.8, lw=2, label=target_name) | ||
| + | ax2.contourf(logreg_grid_x, logreg_grid_y, logreg_pred_grid, alpha=0.3, cmap='Set1') | ||
| + | ax2.set(xlim=(x_min, x_max), ylim=(y_min, y_max)) | ||
| + | ax2.set_title('Regresja logistyczna') | ||
| + | ax2.set_xlabel(feature_names[0]) | ||
| + | ax2.set_ylabel(feature_names[0]) | ||
| + | ax2.legend() | ||
| + | # Wykres dla QDA | ||
| + | ax3 = axes[2] | ||
| + | for color, i, target_name in zip(['navy', 'turquoise', 'darkorange'], [0, 1, 2], target_names): | ||
| + | ax3.scatter(X_scaled[y == i, 0], X_scaled[y == i, 1], color=color, alpha=0.8, lw=2, label=target_name) | ||
| + | ax3.contourf(qda_grid_x, qda_grid_y, qda_pred_grid, alpha=0.3, cmap='Set1') | ||
| + | ax3.set(xlim=(x_min, x_max), ylim=(y_min, y_max)) | ||
| + | ax3.set_title('QDA') | ||
| + | ax3.set_xlabel(feature_names[0]) | ||
| + | ax3.set_ylabel(feature_names[0]) | ||
| + | ax3.legend() | ||
| + | |||
| + | plt.tight_layout() | ||
| + | plt.show() | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | [[Plik:Kosaciec_sep1.png|800px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Plik:Kosaciec_sep2.png|800px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Weryfikacja== | |
| − | + | Ponieważ nie chodzi nam o klasyfikowanie obserwacji już zaklasyfikowanych, tylko nowych, do weryfikacji działania algorytmów stosujemy [https://pl.wikipedia.org/wiki/Sprawdzian_krzy%C5%BCowy sprawdzian krzyżowy] (ang. [https://en.wikipedia.org/wiki/Cross-validation_(statistics) cross-validation]). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Linia 62: | Linia 231: | ||
przykładowy problem: | przykładowy problem: | ||
| − | https://en.wikipedia.org/wiki/MNIST_database | + | https://en.wikipedia.org/wiki/MNIST_database |
| + | |||
===Sieci warstwowe z propagacją wsteczną=== | ===Sieci warstwowe z propagacją wsteczną=== | ||
| − | [[Plik: | + | [[Plik:ANN_3w.jpg|noborder|right|Schemat sieci neuronowej z jedną warstwą ukrytą]] |
| − | Na | + | Na sąsiednim schemacie wagę połączenia przewodzącego pobudzenie od <math>j</math>-tego do <math>i</math>-tego neuronu w <math>k</math>-tej warstwie oznaczono <math>w_{ij}^k</math>. Suma pobudzeń docierających w danej chwili do <math>i</math>-tego neuronu wyniesie |
| − | <math>\sum_{j} w_{ij} n_j | + | <math>\sum_{j} w_{ij} n_j</math> |
Przetwarzanie w neuronie polega na odjęciu od tej sumy charakteryzującego neuron progu <math>\mu_i</math> i podziałaniu na wynik nieliniową funkcją <math>\Phi</math>: | Przetwarzanie w neuronie polega na odjęciu od tej sumy charakteryzującego neuron progu <math>\mu_i</math> i podziałaniu na wynik nieliniową funkcją <math>\Phi</math>: | ||
| Linia 93: | Linia 263: | ||
</math> | </math> | ||
| − | Działanie sieci | + | Działanie tej sieci wygląda następująco: |
* Sygnał wejściowy <math>\vec{x}=\{x_1, x_2, x_3, x_4\}</math> podawany jest na neurony warstwy wejściowej. | * Sygnał wejściowy <math>\vec{x}=\{x_1, x_2, x_3, x_4\}</math> podawany jest na neurony warstwy wejściowej. | ||
| Linia 150: | Linia 320: | ||
<references/> | <references/> | ||
| − | = | + | =Sztuczne sieci neuronowe vs. mózg człowieka= |
[[plik:ANN1.png]] | [[plik:ANN1.png]] | ||
[[plik:ANN2.png]] | [[plik:ANN2.png]] | ||
Aktualna wersja na dzień 14:12, 13 cze 2024
Wnioskowanie_Statystyczne_-_wykład
Spis treści
- 1 Uczenie (maszynowe, ML) nadzorowane (supervised learning)
- 2 Sztuczne sieci neuronowe vs. mózg człowieka
Uczenie (maszynowe, ML) nadzorowane (supervised learning)
Dane mamy podzielone na grupy, szukamy funkcji najlepiej je rozdzielającej, która umożliwi zaklasyfikowanie nowej obserwacji do jednej z tych grup.
Zdefiniowany powyżej cel jest zasadniczo różny od jak najdokładniejszej estymacji p-wartości, która była przedmiotem większości dotychczasowych rozważań.
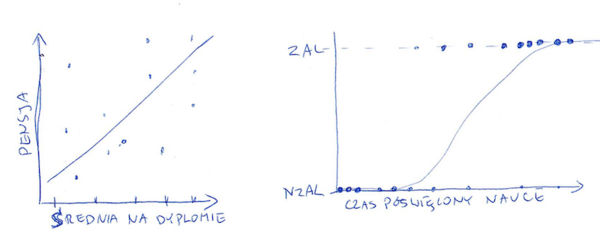
Regresja Logistyczna (Logistic regression, LR)
Omawiana wcześniej regresja liniowa opierała się na linowej zależności między zmienną niezależną [math]x[/math] a zmienną zależną [math]y[/math]
- [math]y = a x + b[/math]
Regresję logistyczną stosujemy w przypadku, gdy zmienna zależna jest jakościowa (wyliczeniowa / czynnikowa / kategoryczna = categorical variable). Nie szacujemy wtedy wartości [math]y[/math] na podstawie [math]x[/math], tylko prawdopodobieństwo przynależności [math]x[/math] do jednej z klas (kategorii) [math]K_i[/math].
- [math]P(K_i | x) = \frac{1}{1 - e^ {-(a x + b)}}[/math]
Podobnie jak w przypadku regresji liniowej, parametry [math]a[/math] i [math]b[/math] możemy estymować metodą największej wiarygodności. Niestety w przypadku LR nie daje się znaleźć rozwiązania analitycznego, do maksymalizacji prawdopodobieństwa a posteriori stosowane są zwykle metody gradientowe.
Liniowa Analiza dyskryminacyjna (Linear Discriminant Analysis, LDA)
Do każdego punktu danych (potencjalnie wielowymiarowych) mamy przypisaną przynależność do jednej z 2 (w klasycznym podejściu Fischera z 1936r.) lub więcej grup/klas. Założenia o danych wejściowych: rozkład normalny, homoskedastyczność, niezależność. Wykorzystywana jest do znalezienia liniowej kombinacji cech, które najlepiej rozróżniają klasy.
Na LDA opierały się też w dużej części techniki psychologicznego mikrotargetowania opracowane przez Michała Kosińskiego, użytego pomimo jego ostrzeżeń (por. artykuł "Psychological targeting as an effective approach to digital mass persuasion") przez Cambridge Analitica.
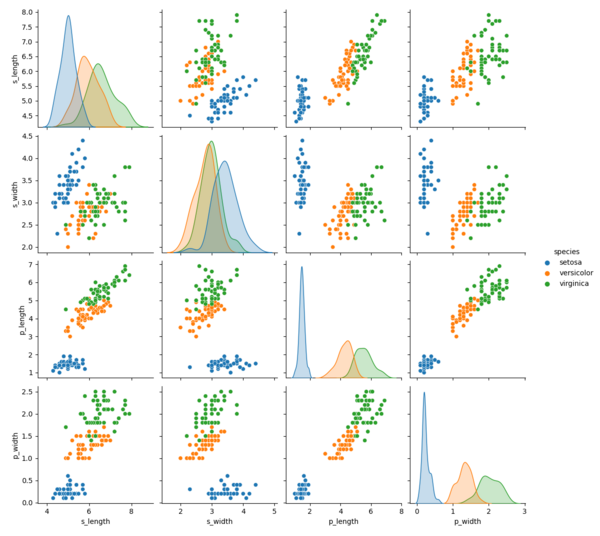
Przykład: gatunki Kosaćca (Iris flower dataset)
| dane |
s_length s_width p_length p_width species 0 5.1 3.5 1.4 0.2 0 1 4.9 3.0 1.4 0.2 0 2 4.7 3.2 1.3 0.2 0 3 4.6 3.1 1.5 0.2 0 4 5.0 3.6 1.4 0.2 0 .. ... ... ... ... ... 145 6.7 3.0 5.2 2.3 2 146 6.3 2.5 5.0 1.9 2 147 6.5 3.0 5.2 2.0 2 148 6.2 3.4 5.4 2.3 2 149 5.9 3.0 5.1 1.8 2 [150 rows x 5 columns] |
| macierz kowariancji |
s_length s_width p_length p_width s_length 0.685694 -0.042434 1.274315 0.516271 s_width -0.042434 0.189979 -0.329656 -0.121639 p_length 1.274315 -0.329656 3.116278 1.295609 p_width 0.516271 -0.121639 1.295609 0.581006 |
| macierz korelacji |
s_length s_width p_length p_width s_length 1.000000 -0.117570 0.871754 0.817941 s_width -0.117570 1.000000 -0.428440 -0.366126 p_length 0.871754 -0.428440 1.000000 0.962865 p_width 0.817941 -0.366126 0.962865 1.000000 |
| kod |
#sepal --- działki kielicha
#Iris --- Kosaciec
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn
from sklearn import datasets
iris=datasets.load_iris()
# convert dataset into a pandas dataframe
df = pd.DataFrame(data = np.c_[iris['data']], columns = iris['feature_names'])
df['species'] = pd.Categorical.from_codes(iris.target, iris.target_names)
df.columns = ['s_length', 's_width', 'p_length', 'p_width','species']
seaborn.pairplot(df, hue="species") #, diag_kind="hist")
plt.show()
df2 = df[df.columns[:-1]]
print('\nkowariancja:\n', df2.cov())
print('\nkorelacja:\n', df2.corr())
|
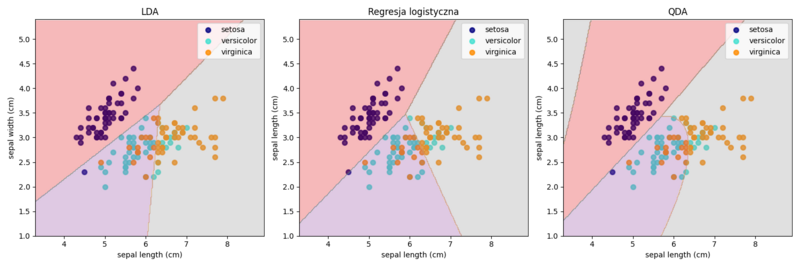
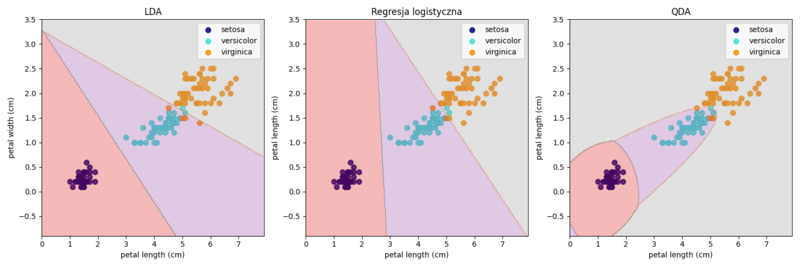
Przykładowe wyniki zastosowania LDA, LR i modelu wyższego rzędu (QDA) do par cech.
Docelowo klasyfikacje robimy oczywiście w oparciu o wszystkie cechy, ale w dwóch wymiarach łatwiej zaobserwować własności metod.
| kod |
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis, QuadraticDiscriminantAnalysis
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
iris = datasets.load_iris()
# Bierzemy tylko dwie cechy dla wizualizacji:
# [:,:2] --- sepal
# [:,2:] --- petal
X = iris.data[:, 2:]
feature_names = iris.feature_names[2:]
target_names = iris.target_names
y = iris.target
X_scaled=X
# Inicjalizacja modeli
lda = LinearDiscriminantAnalysis()
logreg = LogisticRegression()
qda = QuadraticDiscriminantAnalysis()
# Trenowanie modeli
lda.fit(X_scaled, y)
logreg.fit(X_scaled, y)
qda.fit(X_scaled, y)
# Tworzenie siatki punktów dla wizualizacji
h = 0.02 # Rozmiar siatki
x_min, x_max = X_scaled[:, 0].min() - 1, X_scaled[:, 0].max() + 1
y_min, y_max = X_scaled[:, 1].min() - 1, X_scaled[:, 1].max() + 1
lda_grid_x, lda_grid_y = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
logreg_grid_x, logreg_grid_y = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
qda_grid_x, qda_grid_y = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
lda_grid = np.c_[lda_grid_x.ravel(), lda_grid_y.ravel()]
logreg_grid = np.c_[logreg_grid_x.ravel(), logreg_grid_y.ravel()]
qda_grid = np.c_[qda_grid_x.ravel(), qda_grid_y.ravel()]
# Predykcja klas dla punktów na siatce w metodzie LDA
lda_pred_grid = lda.predict(lda_grid)
lda_pred_grid = lda_pred_grid.reshape(lda_grid_x.shape)
# Predykcja klas dla punktów na siatce w metodzie regresji logistycznej
logreg_pred_grid = logreg.predict(logreg_grid)
logreg_pred_grid = logreg_pred_grid.reshape(logreg_grid_x.shape)
# Predykcja klas dla punktów na siatce w metodzie QDA
qda_pred_grid = qda.predict(qda_grid)
qda_pred_grid = qda_pred_grid.reshape(qda_grid_x.shape)
# Wykresy
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# Wykres dla LDA
ax1 = axes[0]
for color, i, target_name in zip(['navy', 'turquoise', 'darkorange'], [0, 1, 2], target_names):
ax1.scatter(X_scaled[y == i, 0], X_scaled[y == i, 1], color=color, alpha=0.8, lw=2, label=target_name)
ax1.contourf(lda_grid_x, lda_grid_y, lda_pred_grid, alpha=0.3, cmap='Set1')
ax1.set(xlim=(x_min, x_max), ylim=(y_min, y_max))
ax1.set_title('LDA')
ax1.set_xlabel(feature_names[0])
ax1.set_ylabel(feature_names[1])
ax1.legend()
# Wykres dla regresji logistycznej
ax2 = axes[1]
for color, i, target_name in zip(['navy', 'turquoise', 'darkorange'], [0, 1, 2], target_names):
ax2.scatter(X_scaled[y == i, 0], X_scaled[y == i, 1], color=color, alpha=0.8, lw=2, label=target_name)
ax2.contourf(logreg_grid_x, logreg_grid_y, logreg_pred_grid, alpha=0.3, cmap='Set1')
ax2.set(xlim=(x_min, x_max), ylim=(y_min, y_max))
ax2.set_title('Regresja logistyczna')
ax2.set_xlabel(feature_names[0])
ax2.set_ylabel(feature_names[0])
ax2.legend()
# Wykres dla QDA
ax3 = axes[2]
for color, i, target_name in zip(['navy', 'turquoise', 'darkorange'], [0, 1, 2], target_names):
ax3.scatter(X_scaled[y == i, 0], X_scaled[y == i, 1], color=color, alpha=0.8, lw=2, label=target_name)
ax3.contourf(qda_grid_x, qda_grid_y, qda_pred_grid, alpha=0.3, cmap='Set1')
ax3.set(xlim=(x_min, x_max), ylim=(y_min, y_max))
ax3.set_title('QDA')
ax3.set_xlabel(feature_names[0])
ax3.set_ylabel(feature_names[0])
ax3.legend()
plt.tight_layout()
plt.show()
|
Weryfikacja
Ponieważ nie chodzi nam o klasyfikowanie obserwacji już zaklasyfikowanych, tylko nowych, do weryfikacji działania algorytmów stosujemy sprawdzian krzyżowy (ang. cross-validation).
Sztuczne sieci neuronowe (ANN )
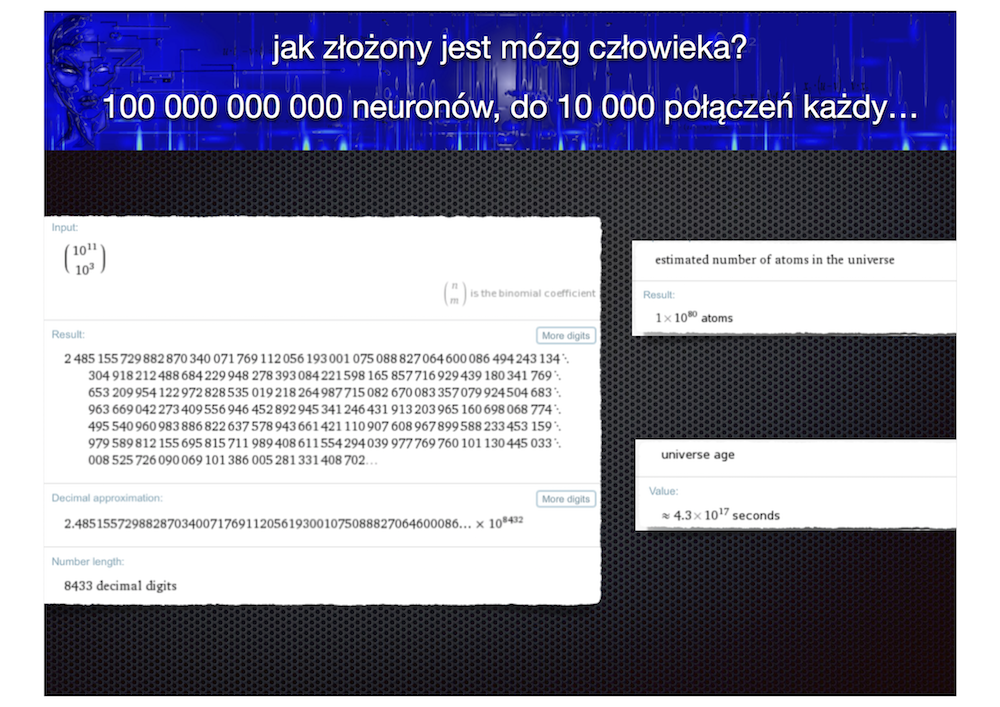
Artificial Neural Networks, ANN powstały w wyniku dążenia do stworzenia systemów naśladujących działanie mózgu. Mózg człowieka składa się z ok. [math]10^{11}-10^{12}[/math] neuronów, każdy z nich posiada ok. [math]10^4[/math] połączeń z innymi neuronami. Ich działanie w największym uproszczeniu można opisać jak następuje:
Potencjał czynnościowy wygenerowany przez neuron propaguje się przez wypustki (akson i dendryty) do innych neuronów. Potencjały docierające do każdego z neuronów sumują się, z wagami zależnymi od siły połączeń. Połączenia między neuronami mogą mieć różną siłę, czyli potencjał czynnościowy generowany ze stałą wartością może mieć różny wkład w zależności od tego, przez jakie połączenie dotarł. Jeśli suma tych potencjałów (po odjęciu wkładu połączeń hamujących) przekroczy ustalony dla danego neuronu próg, to generowany jest potencjał czynnościowy o stałej wartości. Potencjał czynnościowy wygenerowany przez neuron propaguje się...
Ogólnym modelem matematycznym, naśladującym opisane procesy, będzie
sieć złożona z prostych jednostek obliczeniowych, połączonych kanałami komunikacyjnymi zdolnymi do przenoszenia wartości numerycznych. Jednostki działają wyłącznie w oparciu o swe lokalne dane i wejścia z kanałów komunikacyjnych (połączeń).
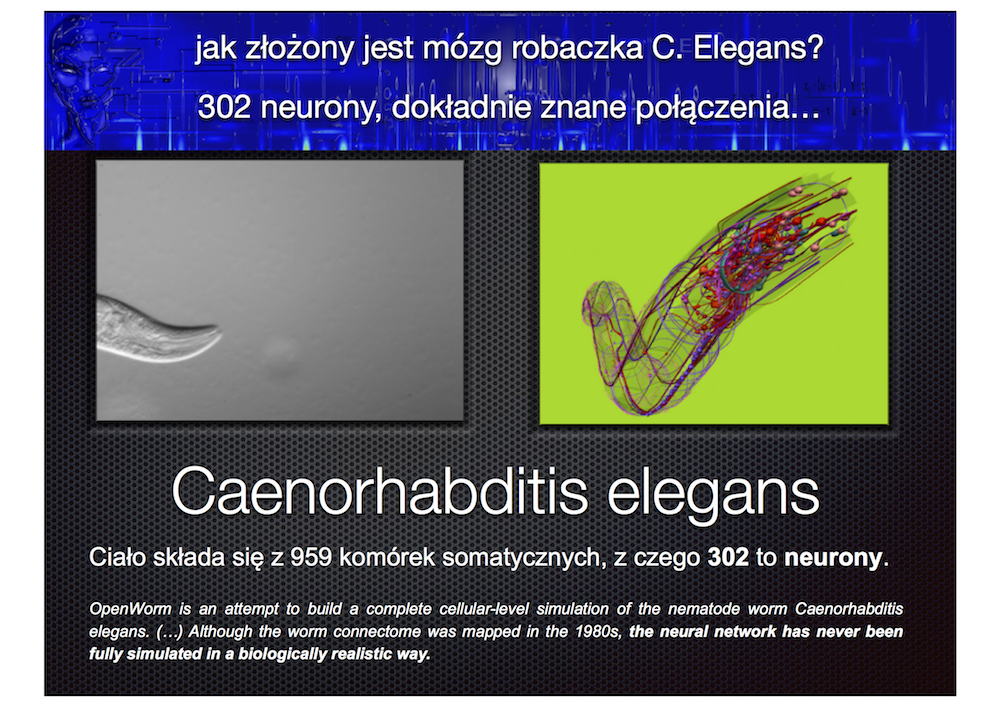
Jednak bliższe badania nad mózgiem człowieka wykazały nieporównanie wyższy niż w przytoczonym opisie stopień złożoności, związany m. in. z wpływem szeregu procesów biochemicznych. I tak np.
do przekazu impulsu z dendrytów do ciała neuronu konieczna jest obecność szeregu neurotransmiterów, czyli cząsteczek przenoszących impuls drogą chemiczną przez szczelinę synaptyczną między dendrytem a ciałem neuronu-adresata[1]. Z kolei generacja potencjału czynnościowego, czyli jak się wydaje podstawowej jednostki przekazu informacji w układzie nerwowym, jest wynikiem złożonych procesów rządzących depolaryzacją błony neuronu. W stanie spoczynku wnętrze neuronu wykazuje potencjał -75 mV względem otoczenia; jest on utrzymywany dzięki aktywności błony neuronu (pompa jonowo-sodowa), utrzymującej wyższe stężenie jonów [math]Na^{+}[/math] na zewnątrz oraz niższe stężenie [math]Cl^{-}[/math] wewnątrz. Neurotransmitery uwolnione z synapsy neuronu wysyłającego impuls powodują otwarcie kanałów przepuszczjących dodatnio naładowane jony sodu ([math]Na^{+}[/math]) do wnętrza neuronu, co zmienia potencjał z -75 mV do +55 mV. Ta depolaryzacja aktywuje kanały sodowe w sąsiednich częściach błony, co powoduje propagację pobudzenia.
Przytoczony powyżej (z pominięciem roli jonów potasu) model Hodgkina-Huxleya jest dziś uważany za bardzo uproszczony. Mimo to, jego stopień komplikacji tak dalece odbiega od sztucznych sieci neuronowych, że nie można ich traktować jako modelu działalności mózgu. Modelowanie prosesów zachodzących w mózgu człowieka to osobna gałąź nauki. Za to właśnie dzięki drastycznym uproszczeniom sztuczne sieci neuronowe (ANN) zyskały efektywność obliczeniową, która w połączeniu z równoległością, tolerancją na błędy i atrakcyjną terminologią doprowadziła do rozpowszechnienia ANN w praktycznych zastosowaniach obliczeniowych.
przykładowy problem:
https://en.wikipedia.org/wiki/MNIST_database
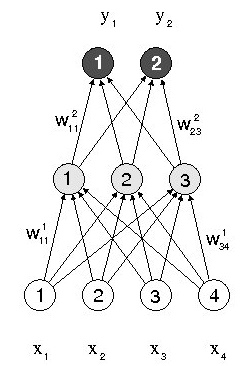
Sieci warstwowe z propagacją wsteczną
Na sąsiednim schemacie wagę połączenia przewodzącego pobudzenie od [math]j[/math]-tego do [math]i[/math]-tego neuronu w [math]k[/math]-tej warstwie oznaczono [math]w_{ij}^k[/math]. Suma pobudzeń docierających w danej chwili do [math]i[/math]-tego neuronu wyniesie
[math]\sum_{j} w_{ij} n_j[/math]
Przetwarzanie w neuronie polega na odjęciu od tej sumy charakteryzującego neuron progu [math]\mu_i[/math] i podziałaniu na wynik nieliniową funkcją [math]\Phi[/math]:
W oryginalnym modelu McCulloha i Pittsa z roku 1943, [math]\Theta(\cdot)[/math] była funkcją progową:
[math] \Theta(x)=\begin{cases} 0 \ dla \ x \lt 0\\ 1\ dla \ x\ge 0 \end{cases}. [/math]
Aktualnie najczęściej stosowaną formą nieliniowości jest funkcja logistyczna
[math] \Theta(x)=\frac{1}{1+e^{-\beta x}} [/math]
Działanie tej sieci wygląda następująco:
- Sygnał wejściowy [math]\vec{x}=\{x_1, x_2, x_3, x_4\}[/math] podawany jest na neurony warstwy wejściowej.
- Aktywacja każdego z neuronów warstwy ukrytej obliczana jest na podstawie równania %i 1. Dla przykładu dla "środkowego" neuronu [math] n_2=\frac{1}{1+e^{-\beta\left(w_{21}^1x_1+w_{22}^1x_2+w_{23}^1x_3+w_{24}^1x_4-\mu_2 \right)}}.[/math]
- Aktywacja neuronów warstwy wyjściowej, czyli odpowiedź sieci na sygnał [math]\vec{x}[/math], obliczana jest analogicznie jak w poprzednim kroku, tylko sygnały wejściowe [math]x_i[/math] zastęują obliczone aktywacje neuronów warstwy ukrytej.
"Inteligencja" sieci zawarta jest w wagach [math]w_{ij}^k[/math] połączeń między kolejnymi warstwami. Clou problemu polega na dobraniu tych wag tak, by realizowały interesujące nas odwzorowanie.
W klasycznym przypadku, nieznane odwzorowanie mamy zadane z pomocą zestawu "przykładów" postaci (wektor wejściowy, prawidłowa klasyfikacja) — oznaczmy je [math](\vec{x}^i, \vec{r}^i)[/math]. Rozważmy dla przykładu konstrukcję sieci rozpoznającej pisane odręcznie litery. Zestaw przykładów stanowić będą mapy bitowe obrazów reprezentujących litery i ich prawidłowe klasyfikacje. Wagi dobierane są w procesie uczenia sieci. Klasyczna procedura przebiega jak następuje:
- Ustalamy architekturę sieci:
- rozmiar warstwy wejściowej jest zwykle zdeterminowany przez rozmiar wektora danych; np w przypadku zapisu pisanych odręcznie liter w postaci obrazów o rozmiarach 15x15 pixeli, rozmiar warstwy wejściowej wyniesie 225 neuronów,
- rozmiar i liczba warstw ukrytych są problemem otwartym; najczęściej używamy jednej warstwy ukrytej, której rozmiar dobieramy empirycznie,
- rozmiar warstwy wyjściowej zależy od sposobu kodowania informacji, którą chcemy na niej odczytywać; w przypadku rozpoznawania dużych liter alfabetu polskiego najlepiej wybrać 35 neuronów wyjściowych: literę "A" reprezentować będzie jedynka na pierwszym neuronie i zera na pozostałych, "B" — jedynka na drugim neuronie itd.
- Inicjalizujemy wagi połączeń [math]w_{ij}^k[/math] przypisując im małe liczby losowe — warto zapamiętać, że w związku z tym każde uruchomienie tego samego algorytmu na tych samych danych może dać w wyniku inną sieć.
- Wybrany losowo ze zbioru uczącego wektor [math]\vec{x}^{in}[/math] prezentujemy na wejściu sieci i obliczamy odpowiedź [math]\vec{n}^{out}[/math].
- Wartości odczytane z neuronów wyjściowych [math]n_i^{out}[/math] porównujemy z "prawidłową odpowiedzią" [math]r_i^{out}[/math]. Jeśli jako funkcję kosztu wybierzemy błąd średniokwadratowy, będzie ona postaci [math] \sum_i (n_i^{out} -r_i^{out})^2[/math]
- Modyfikujemy wagi połączeń kolejnych warstw proporcjonalnie do ich wkładu w dany wynik; jeśli funkcją kosztu będzie błąd średniokwadratowy, wzór na propagację wsteczną błędu otrzymamy wypisując explicite wzór na wartości otrzymane na neuronach wyjściowych w zależności od wag i wartości wejściowych, i różniczkując go po wagach połączeń między kolejnymi warstwami.
- Punkty 3—5 powtarzamy na losowo wybieranych przykładach aż do uzyskania zamierzonego efektu.
Ostatni punkt wymaga podjęcia wysoce nietrywialnej decyzji, od której m.in. zależeć będzie zdolność sieci do generalizacji wiedzy podanej w postaci przykładów.
Metodą uczenia bezpośrednio nakierowaną na optymalizację rozpoznawania wejść spoza zbioru uczącego jest Sprawdzian Krzyżowy (ang. cross-validation).
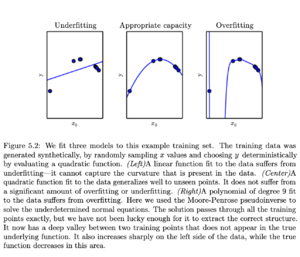
Generalizacja
Głównym celem opisanej powyżej przykładowej konstrukcji nie było rozpoznawanie liter ze zbioru przygotowanego do uczenia sieci (to możnaby osiągnąć znacznie prostszymi metodami), lecz prawidłowa klasyfikacja nowych , nie widzianych przez sieć przypadków. Uzyskanie takiej własności wymaga prawidłowej generalizacji wiedzy "widzianej" w procesie uczenia. Doskonała klasyfikacja przypadków prezentowanych sieci w procesie uczenia nie implikuje wcale poprawnego zachowania sieci na nowych elementach — czasami dla uzyskania prawidłowej generalizacji konieczna jest wręcz pewna tolerancja w stosunku do wyników uzyskiwanych na zbiorze uczącym.
Uzyskaniu poprawnej generalizacji służy m. in. dzielenie zbioru przykładów przeznaczonych do uczenia sieci na zbiór uczący i zbiór kontrolny, nie prezentowany sieci w procesie uczenia (punkty 3—5), i służący wyłącznie do weryfikacji zdolności generalizacji.
Opisany powyżej schemat to zaledwie szkielet metodologii stosowanej w rozwiązywaniu konkretnych problemów. Nawet w swej podstawowej postaci zawiera dwie arbitrarnie wybierane stałe (współczynniki uczenia i bezwładności) od których zależy jego działanie. Metody uczenia stosowane w praktyce oferują ogromą ilość modyfikacji polepszających zbieżność i generalizację.
Polecana lektura: książka "Deep Learning" Ian Goodfellow, Yoshua Bengio and Aaron Courville
- ↑ wybiórcze blokowanie neurotransmiterów przez niektóre leki psychotropowe czy narkotyki prowadzi m. in. do specyficznych zaburzeń działania mózgu