Twierdzenia o splocie i o próbkowaniu (aliasing): Różnice pomiędzy wersjami
| Linia 125: | Linia 125: | ||
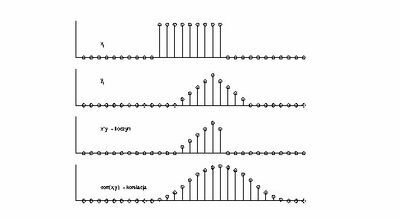
[[Plik:klasyczna_rys_4.jpg|thumb|center|400px|Iloczyn i korelacja dyskretnych sekwencji <math>x</math> i <math>y\ldots</math>]] | [[Plik:klasyczna_rys_4.jpg|thumb|center|400px|Iloczyn i korelacja dyskretnych sekwencji <math>x</math> i <math>y\ldots</math>]] | ||
| + | |||
| + | |||
| + | Konwolucja ma ponadto własność łączności -- dowód można znaleźć np. tutaj: http://planetmath.org/node/39211 | ||
| + | |||
| + | <!-- | ||
| + | Let <math>f</math>, <math>g</math>, and <math>h</math> be measurable functions on the reals, and | ||
| + | suppose the convolutions <math>(f*g)*h</math> and <math>f*(g*h)</math> exist. We must show | ||
| + | that <math>(f*g)*h = f*(g*h)</math>. By the definition of convolution, | ||
| + | <center><math>\begin{matrix} | ||
| + | ((f*g)*h)(u) | ||
| + | &= \int_{\mathbb{R}} (f*g)(x) h(u-x)\,dx | ||
| + | |||
| + | &= \int_{\mathbb{R}} \left[ \int_{\mathbb{R}} f(y) g(x-y)\,dy\right] h(u-x)\,dx | ||
| + | |||
| + | &= \int_{\mathbb{R}} \int_{\mathbb{R}} f(y) g(x-y) h(u-x)\,dy\,dx. | ||
| + | \end{matrix}</math></center> | ||
| + | By Fubini's theorem we can switch the order of integration. Thus | ||
| + | <center><math>\begin{matrix} | ||
| + | ((f*g)*h)(u) | ||
| + | &= \int_{\mathbb{R}} \int_{\mathbb{R}} f(y) g(x-y) h(u-x)\,dx\,dy | ||
| + | |||
| + | &= \int_{\mathbb{R}} f(y) \left[\int_{\mathbb{R}} g(x-y) h(u-x)\,dx\right]\,dy. | ||
| + | \end{matrix}</math></center> | ||
| + | Now let us look at the inner integral. By translation invariance, | ||
| + | <center><math>\begin{matrix} | ||
| + | \int_{\mathbb{R}} g(x-y) h(u-x)\,dx | ||
| + | &= \int_{\mathbb{R}} g((x+y)-y) h(u-(x+y))\,dx | ||
| + | |||
| + | &= \int_{\mathbb{R}} g(x) h((u-y)-x)\,dx | ||
| + | |||
| + | &= (g*h)(u-y). | ||
| + | \end{matrix}</math></center> | ||
| + | So we have shown that | ||
| + | <center><math> | ||
| + | ((f*g)*h)(u) = \int_{\mathbb{R}} f(y)(g*h)(u-y)\,dy, | ||
| + | </math></center> | ||
| + | which by definition is <math>(f*(g*h))(u)</math>. Hence convolution is associative. | ||
| + | |||
| + | --> | ||
| + | |||
| + | |||
| + | |||
| + | |||
<references/> | <references/> | ||
Wersja z 10:04, 4 paź 2015
AS/ Twierdzenie o splocie
Korelacja i splot
Korelacja jest miarą podobieństwa lub wzajemnej zależności. Jeśli mówimy, że występuje korelacja między wydajnością i ceną komputerów, to mamy na myśli stwierdzenie, że droższe komputery mają zwykle większą moc obliczeniową — im mniej przypadków przeciwnych, tym korelacja silniejsza. Silna korelacja sygnałów [math]x[/math] i [math]y[/math] oznacza, że wzrostowi [math]x[/math] towarzyszy najczęściej wzrost [math]y[/math] [math]\left( x_\nearrow\; \rightarrow y_\nearrow \right)[/math]. Jeśli przeważa sytuacja odwrotna [math]\left( x_\nearrow\; \rightarrow y_\searrow \right)[/math] mówimy o korelacji ujemnej.
Miarą współzmienności (kowariancji) dwóch sygnałów jest ich iloczyn. Przed obliczeniem tego iloczynu (w ogólnym przypadku mówimy o jego wartości oczekiwanej) od każdego z sygnałów warto odjąć wartość średnią:
[math] \sigma_{x y}=\int \left(x(t)-\bar{x}\right)\left(y(t)-\bar{y}\right) dt [/math]
Dzięki temu w przypadku, gdy sygnały są od siebie niezależne, [math]\sigma_{x y}[/math] będzie bliska zeru — uniezależnia to miarę kowariancji od wartości średnich sygnałów. Aby otrzymać wartości z przedziału [math][ -1, 1 ][/math] wprowadzamy jako czynnik normalizacyjny wariancję sygnału:
[math] \sigma^2_s=\int\left( s(t)-\bar{s}\right)^2 dt [/math]
Znormalizowaną w ten sposób kowariancję zwiemy korelacją:
[math] \mathrm{korelacja}_{x y} = \frac{\sigma_{x y}}{\sqrt{\sigma^2_x\sigma^2_y}} [/math]
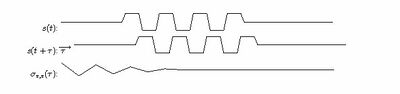
Może się zdarzyć, że dwa sygnały są bardzo podobne, tylko przesunięte względem siebie w czasie. W wykryciu takiej sytuacji pomaga funkcja korelacji wzajemnej, czyli korelacja dwóch sygnałów w funkcji ich wzajemnego przesunięcia. Z kolei autokorelacja to miara korelacji sygnału [math]s(t)[/math] z jego kopią przesuniętą o [math]\tau[/math]. Pomijając normalizację i odejmowanie średnich otrzymamy
[math] \sigma_{s, s}(\tau)=\int s(t) s(t+\tau) dt [/math]
Funkcja autokorelacji będzie miała oczywiście maksimum w zerze, a istnienie innych maksimów związane jest z występowaniem w sygnale okresowo powtarzających się zjawisk. Twierdzenie Wienera-Chinczyna mówi wręcz, że widmo mocy obliczać możemy jako transformatę Fouriera funkcji autokorelacji.
[math] \mathrm{corr}\left(x(t),y(t)\right) = \frac{\sigma^2_{x y}}{\sigma_x \sigma_y} = \frac{\int (x(t)-\mu_x)( y(t)-\mu_y) dt } {\sqrt{ \int (x(t)-\mu_x)^2 dt \int (y(t)-\mu_y)^2 dt }} [/math]
lub
[math] \frac{\sum_i (x_i-\mu_x)(y_i-\mu_y)} {\sqrt{\sum_j (x_j-\mu_x)^2 \sum_k (y_k-\mu_y)^2}} [/math]
Rozważmy transformatę Fouriera funkcji korelacji sygnałów [math]f[/math] i [math]g[/math], dla uproszczenia pomijając normalizację: [math] s(\tau)=\int f(t) g(t+\tau) dt [/math]
[math] =\int e^{-i\omega (t+\tau)} g(t+\tau) \int e^{i\omega t} f(t) dt \; du [/math]
[math] = \int e^{-i\omega u} f(u) du \int e^{i\omega(t)} g(t) dt = \hat{f}(\omega) \overline{\hat{g}(\omega)} [/math]Jak widać, operator korelacji odpowiada w przestrzeni transformat Fouriera iloczynowi transformaty jednego sygnału ze sprzężeniem zespolonym transformaty drugiego.
Twierdzenie o splocie
... czyli splot w przestrzeni czasu odpowiada iloczynowi w przestrzeni transformat Fouriera.
Jest to wynik wygodniejszy od wzoru (1), stąd filtrowanie realizowane jest właśnie z pomocą splotu, który jak widać z równania (1) jest korelacją z sygnałem o odwróconym kierunku czasu.
Dowód:
[math] \hat{s}(\omega) = \int_{-\infty}^{\infty} e^{-i \omega t} s(t) d t = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-i \omega t} f(u) g(t-u) \,d u \,d t [/math] [math] = \int_{-\infty}^{\infty} e^{- i \omega u} f(u) \left( \int_{-\infty}^{\infty} e^{-i \omega (t-u)}g(t-u) dt \right) du [/math]
Całka w nawiasie przebiega od [math]-\infty[/math] do [math]\infty[/math], więc możemy zamienić [math](t-u)[/math] na [math]t[/math]:
[math] = \int_{-\infty}^{\infty} e^{- i \omega u} f(u) \left( \int_{-\infty}^{\infty} e^{i \omega t}g(t) dt \right) du = \hat{f}(\omega) \hat{g}(\omega) [/math]
Konwolucja ma ponadto własność łączności -- dowód można znaleźć np. tutaj: http://planetmath.org/node/39211