Twierdzenia o splocie i o próbkowaniu (aliasing): Różnice pomiędzy wersjami
| (Nie pokazano 22 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
==[[Analiza_sygnałów_-_lecture|AS/]] Twierdzenie o splocie== | ==[[Analiza_sygnałów_-_lecture|AS/]] Twierdzenie o splocie== | ||
| + | |||
| + | |||
| + | [https://phiresky.github.io/convolution-demo/ splot sygnałów — demo] | ||
===Korelacja i splot=== | ===Korelacja i splot=== | ||
| − | Korelacja jest miarą podobieństwa lub wzajemnej zależności. | + | Przypomnijmy z wykładu z Wnioskowania: [[WnioskowanieStatystyczne/Momenty#Kowariancja_i_wsp.C3.B3.C5.82czynnik_korelacji | Korelacja]] |
| + | jest miarą podobieństwa lub wzajemnej zależności. | ||
Jeśli mówimy, że występuje korelacja między wydajnością i ceną | Jeśli mówimy, że występuje korelacja między wydajnością i ceną | ||
komputerów, to mamy na myśli stwierdzenie, że droższe komputery mają | komputerów, to mamy na myśli stwierdzenie, że droższe komputery mają | ||
zwykle większą moc obliczeniową — im mniej przypadków przeciwnych, | zwykle większą moc obliczeniową — im mniej przypadków przeciwnych, | ||
| − | tym korelacja silniejsza. Silna korelacja sygnałów <math>x</math> i | + | tym korelacja silniejsza. |
| + | |||
| + | Silna korelacja sygnałów <math>x</math> i | ||
<math>y</math> oznacza, że wzrostowi <math>x</math> towarzyszy | <math>y</math> oznacza, że wzrostowi <math>x</math> towarzyszy | ||
najczęściej wzrost <math>y</math> <math>\left( x_\nearrow\; | najczęściej wzrost <math>y</math> <math>\left( x_\nearrow\; | ||
| Linia 17: | Linia 23: | ||
mówimy o jego wartości oczekiwanej) od każdego z sygnałów warto odjąć | mówimy o jego wartości oczekiwanej) od każdego z sygnałów warto odjąć | ||
wartość średnią: | wartość średnią: | ||
| + | |||
<math> | <math> | ||
\sigma_{x y}=\int \left(x(t)-\bar{x}\right)\left(y(t)-\bar{y}\right) dt | \sigma_{x y}=\int \left(x(t)-\bar{x}\right)\left(y(t)-\bar{y}\right) dt | ||
</math> | </math> | ||
| + | |||
Dzięki temu w przypadku, gdy sygnały są od siebie niezależne, | Dzięki temu w przypadku, gdy sygnały są od siebie niezależne, | ||
| Linia 26: | Linia 34: | ||
od wartości średnich sygnałów. Aby otrzymać wartości z przedziału <math>[ -1, 1 ]</math> | od wartości średnich sygnałów. Aby otrzymać wartości z przedziału <math>[ -1, 1 ]</math> | ||
wprowadzamy jako czynnik normalizacyjny wariancję sygnału: | wprowadzamy jako czynnik normalizacyjny wariancję sygnału: | ||
| + | |||
<math> | <math> | ||
\sigma^2_s=\int\left( s(t)-\bar{s}\right)^2 dt | \sigma^2_s=\int\left( s(t)-\bar{s}\right)^2 dt | ||
</math> | </math> | ||
| + | |||
Znormalizowaną w ten sposób kowariancję zwiemy korelacją: | Znormalizowaną w ten sposób kowariancję zwiemy korelacją: | ||
| + | |||
<math> | <math> | ||
\mathrm{korelacja}_{x y} = \frac{\sigma_{x y}}{\sqrt{\sigma^2_x\sigma^2_y}} | \mathrm{korelacja}_{x y} = \frac{\sigma_{x y}}{\sqrt{\sigma^2_x\sigma^2_y}} | ||
</math> | </math> | ||
| + | |||
Może się zdarzyć, że dwa sygnały są bardzo podobne, tylko przesunięte | Może się zdarzyć, że dwa sygnały są bardzo podobne, tylko przesunięte | ||
| Linia 43: | Linia 55: | ||
sygnału <math>s(t)</math> z jego kopią przesuniętą o <math>\tau</math>. Pomijając normalizację | sygnału <math>s(t)</math> z jego kopią przesuniętą o <math>\tau</math>. Pomijając normalizację | ||
i odejmowanie średnich otrzymamy | i odejmowanie średnich otrzymamy | ||
| + | |||
<math> | <math> | ||
\sigma_{s, s}(\tau)=\int s(t) s(t+\tau) dt | \sigma_{s, s}(\tau)=\int s(t) s(t+\tau) dt | ||
</math> | </math> | ||
| + | |||
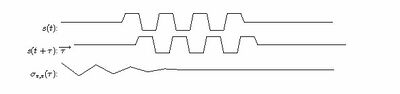
[[Plik:klasyczna_rys_3.jpg|thumb|center|400px|Od góry: sygnał <math>s(t)</math>, ten sam sygnał przesunięty w czasie o <math>\tau</math>, i jego funkcja autokorelacji.]] | [[Plik:klasyczna_rys_3.jpg|thumb|center|400px|Od góry: sygnał <math>s(t)</math>, ten sam sygnał przesunięty w czasie o <math>\tau</math>, i jego funkcja autokorelacji.]] | ||
| + | |||
Funkcja autokorelacji będzie miała oczywiście maksimum w zerze, a istnienie | Funkcja autokorelacji będzie miała oczywiście maksimum w zerze, a istnienie | ||
| Linia 54: | Linia 69: | ||
powtarzających się zjawisk. [[Model_autoregresyjny_(AR)#Twierdzenie Wienera-Chinczyna|Twierdzenie Wienera-Chinczyna]] mówi wręcz, | powtarzających się zjawisk. [[Model_autoregresyjny_(AR)#Twierdzenie Wienera-Chinczyna|Twierdzenie Wienera-Chinczyna]] mówi wręcz, | ||
że widmo mocy obliczać możemy jako [[Przekształcenie Fouriera|transformatę Fouriera]] funkcji autokorelacji. | że widmo mocy obliczać możemy jako [[Przekształcenie Fouriera|transformatę Fouriera]] funkcji autokorelacji. | ||
| + | |||
<math> | <math> | ||
| Linia 60: | Linia 76: | ||
{\sqrt{ \int (x(t)-\mu_x)^2 dt \int (y(t)-\mu_y)^2 dt }} | {\sqrt{ \int (x(t)-\mu_x)^2 dt \int (y(t)-\mu_y)^2 dt }} | ||
</math> | </math> | ||
| + | |||
lub | lub | ||
| + | |||
<math> | <math> | ||
| Linia 67: | Linia 85: | ||
{\sqrt{\sum_j (x_j-\mu_x)^2 \sum_k (y_k-\mu_y)^2}} | {\sqrt{\sum_j (x_j-\mu_x)^2 \sum_k (y_k-\mu_y)^2}} | ||
</math> | </math> | ||
| + | |||
Rozważmy [[Przekształcenie Fouriera|transformatę Fouriera]] funkcji korelacji sygnałów <math>f</math> i <math>g</math>, dla uproszczenia pomijając normalizację: | Rozważmy [[Przekształcenie Fouriera|transformatę Fouriera]] funkcji korelacji sygnałów <math>f</math> i <math>g</math>, dla uproszczenia pomijając normalizację: | ||
| + | |||
| + | |||
<math> | <math> | ||
s(\tau)=\int f(t) g(t+\tau) dt | s(\tau)=\int f(t) g(t+\tau) dt | ||
</math> | </math> | ||
| + | |||
<equation id="eq:29"> | <equation id="eq:29"> | ||
| Linia 78: | Linia 100: | ||
\int e^{-i\omega \tau} \left( \int f(t) g(t+\tau) dt \right) d\tau | \int e^{-i\omega \tau} \left( \int f(t) g(t+\tau) dt \right) d\tau | ||
</math> | </math> | ||
| + | |||
| + | |||
| + | <math> | ||
| + | \hat{s}(\omega)= | ||
| + | \int e^{i\omega t} e^{-i\omega t} e^{-i\omega \tau} \left( \int f(t) g(t+\tau) dt \right) d\tau | ||
| + | </math> | ||
| + | |||
| + | |||
<math> | <math> | ||
| − | =\int e^{-i\omega (t+\tau)} g(t+\tau) \int e^{i\omega t} f(t) | + | =\int e^{-i\omega (t+\tau)} g(t+\tau)\; d\tau \int e^{i\omega t} f(t) \; dt |
</math> | </math> | ||
| + | |||
| + | |||
<math> | <math> | ||
| − | = \int e^{-i\omega u} | + | = \int e^{-i\omega u} g(u) du \int e^{i\omega t } f(t) dt = |
| − | \hat{ | + | \hat{g}(\omega) \overline{\hat{f}(\omega)} |
</math> | </math> | ||
</equation> | </equation> | ||
| + | |||
Jak widać, operator korelacji odpowiada w przestrzeni transformat | Jak widać, operator korelacji odpowiada w przestrzeni transformat | ||
Fouriera iloczynowi transformaty jednego sygnału ze sprzężeniem | Fouriera iloczynowi transformaty jednego sygnału ze sprzężeniem | ||
| − | zespolonym transformaty drugiego. | + | zespolonym transformaty drugiego. |
===Twierdzenie o splocie=== | ===Twierdzenie o splocie=== | ||
| + | |||
| + | |||
<equation id="eq:30"> | <equation id="eq:30"> | ||
| − | <math> | + | <math> \displaystyle |
s(t) = \int_{-\infty}^{\infty} f(u) g(t-u) du | s(t) = \int_{-\infty}^{\infty} f(u) g(t-u) du | ||
\;\; \Longrightarrow \;\;\; | \;\; \Longrightarrow \;\;\; | ||
| Linia 99: | Linia 134: | ||
</math> | </math> | ||
</equation> | </equation> | ||
| + | |||
| + | |||
... czyli splot w przestrzeni czasu odpowiada iloczynowi w przestrzeni transformat Fouriera. | ... czyli splot w przestrzeni czasu odpowiada iloczynowi w przestrzeni transformat Fouriera. | ||
| Linia 105: | Linia 142: | ||
splotu, który jak widać z równania <xr id="eq:29">(%i)</xr> jest korelacją | splotu, który jak widać z równania <xr id="eq:29">(%i)</xr> jest korelacją | ||
z sygnałem o odwróconym kierunku czasu. | z sygnałem o odwróconym kierunku czasu. | ||
| + | |||
'''Dowód''': | '''Dowód''': | ||
| − | <math> | + | |
| + | <math>\displaystyle | ||
\hat{s}(\omega) = \int_{-\infty}^{\infty} e^{-i \omega t} s(t) d t = | \hat{s}(\omega) = \int_{-\infty}^{\infty} e^{-i \omega t} s(t) d t = | ||
\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-i \omega t} | \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-i \omega t} | ||
f(u) g(t-u) \,d u \,d t | f(u) g(t-u) \,d u \,d t | ||
</math> | </math> | ||
| − | <math> | + | |
| + | |||
| + | <math>\displaystyle | ||
= \int_{-\infty}^{\infty} e^{- i \omega u} f(u) \left( \int_{-\infty}^{\infty} e^{-i \omega (t-u)}g(t-u) dt \right) du | = \int_{-\infty}^{\infty} e^{- i \omega u} f(u) \left( \int_{-\infty}^{\infty} e^{-i \omega (t-u)}g(t-u) dt \right) du | ||
</math> | </math> | ||
| + | |||
Całka w nawiasie przebiega od <math>-\infty</math> do <math>\infty</math>, więc możemy zamienić <math>(t-u)</math> na <math>t</math>: | Całka w nawiasie przebiega od <math>-\infty</math> do <math>\infty</math>, więc możemy zamienić <math>(t-u)</math> na <math>t</math>: | ||
| − | <math> | + | |
| − | = \int_{-\infty}^{\infty} e^{- i \omega u} f(u) \left( \int_{-\infty}^{\infty} e^{i \omega t}g(t) dt \right) du = | + | <math>\displaystyle |
| + | = \int_{-\infty}^{\infty} e^{- i \omega u} f(u) \left( \int_{-\infty}^{\infty} e^{- i \omega t}g(t) dt \right) du = | ||
\hat{f}(\omega) \hat{g}(\omega) | \hat{f}(\omega) \hat{g}(\omega) | ||
</math> | </math> | ||
| Linia 127: | Linia 170: | ||
| − | Splot ma ponadto własność łączności | + | Splot ma ponadto własność łączności, czyli <math>(f*g)*h = f*(g*h)</math>. Z definicji |
| + | |||
| − | + | <math>\displaystyle | |
| − | |||
| − | |||
| − | |||
| − | |||
((f*g)*h)(u) | ((f*g)*h)(u) | ||
| − | + | = \int_{-\infty}^{\infty} (f*g)(x) h(u-x)\,dx | |
| + | </math> | ||
| + | |||
| + | |||
| + | <math>\displaystyle | ||
| + | = \int_{-\infty}^{\infty} \left[ \int_{-\infty}^{\infty} f(y) g(x-y)\,dy\right] h(u-x)\,dx | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math>\displaystyle | ||
| + | = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(y) g(x-y) h(u-x)\,dy\,dx. | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Zmieniamy kolejność całkowania na mocy twierdzenia Fubiniego: | ||
| − | |||
| − | + | <math>\displaystyle | |
| − | |||
| − | |||
| − | |||
((f*g)*h)(u) | ((f*g)*h)(u) | ||
| − | + | = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(y) g(x-y) h(u-x)\,dx\,dy | |
| + | = \int_{-\infty}^{\infty} f(y) \left[\int_{-\infty}^{\infty} g(x-y) h(u-x)\,dx\right]\,dy. | ||
| + | </math> | ||
| + | |||
| + | |||
| + | przyjrzyjmy się całce w nawiasie kwadratowym; całki są po <math>\mathbb{R}</math>, więc na mocy niezmienności względem przesunięcia możemy przesunąć argument <math>x</math> o <math>-y</math> czyli <math>x \rightarrow (x+y)</math>: | ||
| + | |||
| + | |||
| + | <math>\displaystyle | ||
| + | \int_{-\infty}^\infty g(x-y) h(u-x)\,dx | ||
| + | = \int_{-\infty}^\infty g((x+y)-y) h(u-(x+y))\,dx | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math>\displaystyle | ||
| + | = \int_{-\infty}^{\infty} g(x) h((u-y)-x)\,dx = (g*h)(u-y). | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Tak więc pokazaliśmy, że | ||
| + | |||
| − | + | <math>\displaystyle | |
| − | + | ((f*g)*h)(u) = \int_{-\infty}^{\infty} f(y)(g*h)(u-y)\,dy | |
| − | + | = (f*(g*h))(u)</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Aktualna wersja na dzień 09:14, 27 paź 2023
AS/ Twierdzenie o splocie
Korelacja i splot
Przypomnijmy z wykładu z Wnioskowania: Korelacja jest miarą podobieństwa lub wzajemnej zależności. Jeśli mówimy, że występuje korelacja między wydajnością i ceną komputerów, to mamy na myśli stwierdzenie, że droższe komputery mają zwykle większą moc obliczeniową — im mniej przypadków przeciwnych, tym korelacja silniejsza.
Silna korelacja sygnałów [math]x[/math] i [math]y[/math] oznacza, że wzrostowi [math]x[/math] towarzyszy najczęściej wzrost [math]y[/math] [math]\left( x_\nearrow\; \rightarrow y_\nearrow \right)[/math]. Jeśli przeważa sytuacja odwrotna [math]\left( x_\nearrow\; \rightarrow y_\searrow \right)[/math] mówimy o korelacji ujemnej.
Miarą współzmienności (kowariancji) dwóch sygnałów jest ich iloczyn. Przed obliczeniem tego iloczynu (w ogólnym przypadku mówimy o jego wartości oczekiwanej) od każdego z sygnałów warto odjąć wartość średnią:
[math]
\sigma_{x y}=\int \left(x(t)-\bar{x}\right)\left(y(t)-\bar{y}\right) dt
[/math]
Dzięki temu w przypadku, gdy sygnały są od siebie niezależne,
[math]\sigma_{x y}[/math] będzie bliska zeru — uniezależnia to miarę kowariancji
od wartości średnich sygnałów. Aby otrzymać wartości z przedziału [math][ -1, 1 ][/math]
wprowadzamy jako czynnik normalizacyjny wariancję sygnału:
[math]
\sigma^2_s=\int\left( s(t)-\bar{s}\right)^2 dt
[/math]
Znormalizowaną w ten sposób kowariancję zwiemy korelacją:
[math]
\mathrm{korelacja}_{x y} = \frac{\sigma_{x y}}{\sqrt{\sigma^2_x\sigma^2_y}}
[/math]
Może się zdarzyć, że dwa sygnały są bardzo podobne, tylko przesunięte
względem siebie w czasie. W wykryciu takiej sytuacji pomaga funkcja
korelacji wzajemnej, czyli korelacja dwóch sygnałów w funkcji
ich wzajemnego przesunięcia. Z kolei autokorelacja to miara korelacji
sygnału [math]s(t)[/math] z jego kopią przesuniętą o [math]\tau[/math]. Pomijając normalizację
i odejmowanie średnich otrzymamy
[math]
\sigma_{s, s}(\tau)=\int s(t) s(t+\tau) dt
[/math]
Funkcja autokorelacji będzie miała oczywiście maksimum w zerze, a istnienie
innych maksimów związane jest z występowaniem w sygnale okresowo
powtarzających się zjawisk. Twierdzenie Wienera-Chinczyna mówi wręcz,
że widmo mocy obliczać możemy jako transformatę Fouriera funkcji autokorelacji.
[math]
\mathrm{corr}\left(x(t),y(t)\right) = \frac{\sigma^2_{x y}}{\sigma_x \sigma_y} =
\frac{\int (x(t)-\mu_x)( y(t)-\mu_y) dt }
{\sqrt{ \int (x(t)-\mu_x)^2 dt \int (y(t)-\mu_y)^2 dt }}
[/math]
lub
[math]
\frac{\sum_i (x_i-\mu_x)(y_i-\mu_y)}
{\sqrt{\sum_j (x_j-\mu_x)^2 \sum_k (y_k-\mu_y)^2}}
[/math]
Rozważmy transformatę Fouriera funkcji korelacji sygnałów [math]f[/math] i [math]g[/math], dla uproszczenia pomijając normalizację:
[math]
s(\tau)=\int f(t) g(t+\tau) dt
[/math]
[math]
\hat{s}(\omega)=
\int e^{i\omega t} e^{-i\omega t} e^{-i\omega \tau} \left( \int f(t) g(t+\tau) dt \right) d\tau
[/math]
[math]
=\int e^{-i\omega (t+\tau)} g(t+\tau)\; d\tau \int e^{i\omega t} f(t) \; dt
[/math]
Jak widać, operator korelacji odpowiada w przestrzeni transformat
Fouriera iloczynowi transformaty jednego sygnału ze sprzężeniem
zespolonym transformaty drugiego.
Twierdzenie o splocie
... czyli splot w przestrzeni czasu odpowiada iloczynowi w przestrzeni transformat Fouriera.
Jest to wynik wygodniejszy od wzoru (1), stąd filtrowanie realizowane jest właśnie z pomocą splotu, który jak widać z równania (1) jest korelacją z sygnałem o odwróconym kierunku czasu.
Dowód:
[math]\displaystyle
\hat{s}(\omega) = \int_{-\infty}^{\infty} e^{-i \omega t} s(t) d t =
\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-i \omega t}
f(u) g(t-u) \,d u \,d t
[/math]
[math]\displaystyle
= \int_{-\infty}^{\infty} e^{- i \omega u} f(u) \left( \int_{-\infty}^{\infty} e^{-i \omega (t-u)}g(t-u) dt \right) du
[/math]
Całka w nawiasie przebiega od [math]-\infty[/math] do [math]\infty[/math], więc możemy zamienić [math](t-u)[/math] na [math]t[/math]:
[math]\displaystyle
= \int_{-\infty}^{\infty} e^{- i \omega u} f(u) \left( \int_{-\infty}^{\infty} e^{- i \omega t}g(t) dt \right) du =
\hat{f}(\omega) \hat{g}(\omega)
[/math]
Splot ma ponadto własność łączności, czyli [math](f*g)*h = f*(g*h)[/math]. Z definicji
[math]\displaystyle
((f*g)*h)(u)
= \int_{-\infty}^{\infty} (f*g)(x) h(u-x)\,dx
[/math]
[math]\displaystyle
= \int_{-\infty}^{\infty} \left[ \int_{-\infty}^{\infty} f(y) g(x-y)\,dy\right] h(u-x)\,dx
[/math]
[math]\displaystyle
= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(y) g(x-y) h(u-x)\,dy\,dx.
[/math]
Zmieniamy kolejność całkowania na mocy twierdzenia Fubiniego:
[math]\displaystyle
((f*g)*h)(u)
= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(y) g(x-y) h(u-x)\,dx\,dy
= \int_{-\infty}^{\infty} f(y) \left[\int_{-\infty}^{\infty} g(x-y) h(u-x)\,dx\right]\,dy.
[/math]
przyjrzyjmy się całce w nawiasie kwadratowym; całki są po [math]\mathbb{R}[/math], więc na mocy niezmienności względem przesunięcia możemy przesunąć argument [math]x[/math] o [math]-y[/math] czyli [math]x \rightarrow (x+y)[/math]:
[math]\displaystyle
\int_{-\infty}^\infty g(x-y) h(u-x)\,dx
= \int_{-\infty}^\infty g((x+y)-y) h(u-(x+y))\,dx
[/math]
[math]\displaystyle
= \int_{-\infty}^{\infty} g(x) h((u-y)-x)\,dx = (g*h)(u-y).
[/math]
Tak więc pokazaliśmy, że
[math]\displaystyle
((f*g)*h)(u) = \int_{-\infty}^{\infty} f(y)(g*h)(u-y)\,dy
= (f*(g*h))(u)[/math]