WnioskowanieStatystyczne/CLT: Różnice pomiędzy wersjami
(Utworzono nową stronę " ==Centralne Twierdzenie Graniczne== Rozkład Gaussa pełni w statystyce bardzo znaczącą rolę ze względu na ''Centralne Twierdzenie Graniczne'' , według którego r...") |
|||
| (Nie pokazano 152 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
| − | + | [[Wnioskowanie_Statystyczne_-_wykład]] | |
| − | Rozkład Gaussa | + | ==Rozkład Gaussa== |
| − | + | ||
| − | + | Rozkład Gaussa (zwany też rozkładem normalnym lub krzywą dzwonową) zależy od | |
| − | + | parametrów <math>\mu</math> i <math>\sigma</math>. Jego gęstość prawdopodobieństwa określona jest wzorem: | |
| − | + | ||
| − | + | <center><math display="block"> | |
| − | + | p(x)=N(\mu, \sigma)= \frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-(x-\mu )^{2}}{2\sigma ^{2}}}. | |
| − | + | </math></center> | |
| − | + | ||
| + | Parametry te są tak dobrane, że wartość oczekiwana wynosi | ||
| + | <math>\mu</math>, a wariancja <math>\sigma^2</math>. | ||
| + | |||
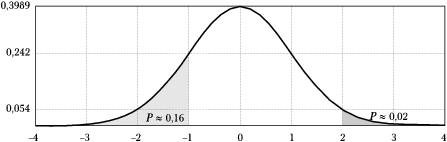
| + | [[Plik:Rozklad_gaussa.png|600px|thumb|left|<math>N(0,1)</math>, czyli | ||
| + | standardowy rozkład Gaussa o zerowej średniej (<math>\mu=0</math>) i | ||
| + | jednostkowej wariancji (<math>\sigma=1</math>).]] | ||
| + | |||
| + | Rozkład Gaussa dla zerowej wartości oczekiwanej i jednostkowej | ||
| + | wariancji (<math>\mu=0, \sigma^2=1</math>) zwiemy | ||
| + | ''standardowym rozkładem Gaussa'' | ||
| + | i oznaczamy zwykle <math>N(0,1)</math>. | ||
| + | Na wykresie zaznaczono na nim m. in. wartość całki od <math>-\infty</math> do | ||
| + | <math>-1</math>, czyli prawdopodobieństwo, że wylosowana z tego | ||
| + | rozkładu liczba będzie mniejsza niż <math>-1</math>. Jak widać, wynosi | ||
| + | ono ok. 16%, a jeśli weźmiemy pod uwagę również wartości większe od 1, | ||
| + | będzie to aż 32%! Oznacza to, że przy losowaniu wielu liczb z tego | ||
| + | rozkładu niemal 1/3 wyników może znaleźć się w odległości | ||
| + | większej niż <math>\sigma</math> od wartości oczekiwanej. | ||
| + | |||
| + | <equation id="eq:80"> | ||
| + | <math> | ||
| + | x\in N(\mu,\sigma)\quad \Rightarrow \quad | ||
| + | \begin{cases} | ||
| + | P(\left| x-\mu \right| \geq \sigma )\approx 0,\!317,\\ | ||
| + | P(\left| x-\mu \right| \geq 2\sigma )\ \approx 0,\!046,\\ | ||
| + | \ P(\left| x-\mu \right| \geq 3\sigma )\approx 0,\!003. | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | </equation> | ||
| + | |||
| + | <!-- Gęstość prawdopodobieństwa dana równaniem | ||
| + | <xr id="eq:78">(%i)</xr> zanika w nieskończoności tylko | ||
| + | asymptotycznie, i dlatego w świetle tego rozkładu prawdopodobieństwo | ||
| + | wylosowania ''dowolnej'' wartości będzie niezerowe (choć dla | ||
| + | większości niezmiernie małe). Prowadzi to czasem do paradoksów, jak | ||
| + | np. niezerowe prawdopodobieństwo ujemnej masy.<ref>Gaussowski | ||
| + | rozkład pomiarów jakiejkolwiek masy, określony dodatnimi wartościami | ||
| + | <math>\mu</math> i <math>\sigma</math>, będzie wykazywał nieujemne — | ||
| + | choć zapewne bardzo małe — prawdopodobieństwo również dla ujemnych | ||
| + | wartości zmiennej losowej, którą w tym przypadku będzie mierzona | ||
| + | masa.</ref> Jest to cena za korzystanie ze zwięzłej i eleganckiej | ||
| + | postaci analitycznej rozkładu. --> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Rozkład Gaussa pełni w statystyce bardzo znaczącą rolę ze względu na ''Centralne Twierdzenie Graniczne'', mówiące o asysmptotycznym rozkładzie sumy dużej liczby niezależnych zmiennych losowych, których rozkłady spełniają pewne warunki. Udowodnimy je w najprostszym przypadku, kiedy wszystkie te zmienne pochodzą z tego samego rozkładu gęstości prawdopodobieństwa. Na potrzeby tego dowodu musimy najpierw wprowadzić pojęcie funkcji charakterystycznej. | |
| − | |||
| − | |||
| − | |||
| − | + | <!-- | |
| + | Rozkład Gaussa pełni w statystyce bardzo znaczącą rolę ze względu na | ||
| + | ''Centralne Twierdzenie Graniczne'', według którego rozkład zmiennej losowej <math>y</math>, będącej sumą dużej liczby zmiennych losowych <math>x_i</math> (czyli <math>y=\sum_{i=1}^{N} x_i</math>) dąży, przy liczbie sumowanych zmiennych dążących do | ||
| + | nieskończoności (czyli <math>N\rightarrow\infty</math>), do rozkładu Gaussa. | ||
| + | Poniżej przytoczymy dowód tego | ||
| + | twierdzenia dla uproszczonego przypadku sumy zmiennych pochodzących z | ||
| + | tego samego rozkładu.<ref>Dokładniejsze sformułowania Twierdzenia | ||
| + | można znaleźć np. w [http://www.wnt.com.pl/product.php?action=0&prod_id=1488&hot=1 książce "Probabilistyka. Rachunek Prawdopodobieństwa. Statystyka matematyczna. Procesy stochastyczne" Agnieszki i Edmunda Plucińskich].</ref> | ||
| + | --> | ||
| − | == | + | ==Funkcja charakterystyczna rozkładu prawdopodobieństwa== |
| − | + | Dla zmiennej losowej <math>x</math> jest to wartość oczekiwana wyrażenia <math>e^{itx}</math>, gdzie <math>i=\sqrt{-1}</math>. Dla rozkładów ciągłych jest to [[Przekształcenie_Fouriera|transformata Fouriera]] funkcji gęstości prawdopodobieństwa <math>f(x)</math>: | |
| − | |||
| − | |||
<center><math> | <center><math> | ||
| − | \ | + | \phi_x (t)=E(e^{itx})=\underset{-\infty }{\overset{\infty }{\int }} |
e^{itx}f\left( x\right) dx | e^{itx}f\left( x\right) dx | ||
</math></center> | </math></center> | ||
| − | < | + | Użyteczne będą poniższe związki, które wyprowadzić można bezpośrednio z definicji: |
| − | <math>\ | + | |
| − | + | ====Funkcja charakterystyczna rozkładu sumy zmiennych niezależnych==== | |
| + | Dla ''niezależnych'' zmiennych <math>x</math> i <math>y</math>: | ||
| + | <equation id="eq:85"> | ||
| + | <center> | ||
| + | <math> | ||
| + | w=x+y\Rightarrow \phi _{w}(t) | ||
| + | =\phi _{x}\left( t\right) \cdot \phi_{y}(t). | ||
| + | </math> | ||
| + | </center> | ||
| + | </equation> | ||
| + | |||
| + | Dowód: | ||
| + | |||
| + | <math> | ||
| + | \phi _{w}(t) | ||
| + | = E(e^{it(x+y)})=E(e^{itx}\cdot e^{ity}) | ||
| + | = E(e^{itx})\cdot E(e^{ity})=\phi _{x}\left( t\right) \cdot \phi_{y}(t). | ||
</math> | </math> | ||
| − | |||
| − | |||
| + | ====Pochodna funkcji charakterystycznej==== | ||
| + | Bezpośrednio z definicji (różniczkujemy po <math>dt</math>, więc przy każdym różniczkowaniu spada nam z wykładnika <math>i x</math>, <math>x</math> zostaje pod całką a <math>i</math> jako stała wychodzi przed całkę) widać, że: | ||
<equation id="eq:pochodna_funkcji_tworzacej"> | <equation id="eq:pochodna_funkcji_tworzacej"> | ||
<center><math> | <center><math> | ||
| Linia 50: | Linia 105: | ||
</equation> | </equation> | ||
| − | + | ====Związek pochodnej funkcji charakterystycznej z momentami zmiennej losowej==== | |
| − | + | <math>n</math>-ta pochodna funkcji charakterystycznej w zerze (czyli dla <math>t=0</math>) wynosi | |
| − | |||
<equation id="eq:84"> | <equation id="eq:84"> | ||
<center><math> | <center><math> | ||
| Linia 62: | Linia 116: | ||
</equation> | </equation> | ||
| − | + | ==Twierdzenie Lindeberga–Lévy'ego== | |
| − | <equation id="eq: | + | Zakładamy, że <math>x_{i}</math> są niezależnymi zmiennymi podlegającymi (dowolnemu) rozkładowi o skończonej wartości oczekiwanej <math>\mu</math> i wariancji <math>\sigma^{2}</math>, czyli wszystkie sumowane zmienne <math>x_i</math> pochodzą z tego samego rozkładu prawdopodobieństwa, o którym nie zakładamy nic ponad to, że ma skończone <math>\mu</math> i <math>\sigma</math>. |
| + | Wielkość | ||
| + | |||
| + | <center> | ||
| + | <equation id="eq:82"> <math> | ||
| + | S=\dfrac{ \sum\limits_{i=1}^{n}x_{i}\; -\; n\mu}{\sigma \sqrt{n}} | ||
| + | </math> </equation> | ||
| + | </center> | ||
| + | |||
| + | dla <math>n\rightarrow \infty</math> zbiega do rozkładu normalnego o zerowej wartości średniej i jednostkowej wariancji. | ||
| + | |||
| + | |||
| + | |||
| + | ===Dowód twierdzenia Lindeberga–Lévy'ego=== | ||
| + | Rozważmy zmienną <math>y_i</math> o zerowej wartości oczekiwanej i jednostkowej wariancji | ||
| + | <center><math> | ||
| + | y_{i} = \dfrac{x_{i}-\mu}{\sigma} . | ||
| + | </math></center> | ||
| + | |||
| + | Funkcję charakterystyczną rozkładu zmiennej <math>y_i</math> | ||
| + | <center><math>\phi_{y_i}(z) = E(e^{i z y_i}) </math></center> | ||
| + | możemy rozwinąć w szereg Taylora wokół <math>z=0</math> | ||
| + | <equation id="eq:86"> | ||
<center><math> | <center><math> | ||
| − | + | \phi_{y_i}(z)=\underset{n=0}{\overset{\infty }{\sum }}\frac{\phi^{(n)}(0)}{n!}z^n | |
| − | |||
| − | |||
</math></center> | </math></center> | ||
</equation> | </equation> | ||
| + | Z wyprowadzonej wcześniej własności funkcji charakterystycznej <xr id="eq:84">(%i)</xr> | ||
| + | <math> | ||
| + | \phi^{(n)}(0)= | ||
| + | i^{n}E(x^{n}) | ||
| + | </math> | ||
| + | wynika, że | ||
| + | |||
| + | <math>\phi_{y_i}^{(0)}(0)=1</math>, | ||
| + | |||
| + | <math>\phi_{y_i}^{(1)}(0)=0</math> (wartość oczekiwana), | ||
| + | |||
| + | <math>\phi_{y_i}^{(2)}(0)=-1</math> (<math>i^2</math> * wariancja), | ||
| − | + | czyli funkcja charakterystyczna zmiennej <math>y_i</math> rozwinięta w szereg Taylora <xr id="eq:86">(%i)</xr> do wyrazów drugiego rzędu będzie miała postać | |
| − | + | <equation id="eq:87"> | |
<center><math> | <center><math> | ||
| − | \ | + | \phi_{y_i}(z)=1-\frac{z^{2}}{2}+\cdots . |
| − | |||
| − | |||
</math></center> | </math></center> | ||
| − | + | </equation> | |
| + | |||
| + | |||
| + | Wrócmy do występującej w twierdzeniu sumy <math>S</math> | ||
| + | |||
| + | <math> | ||
| + | S=\dfrac{ \sum\limits_{i=1}^{n}x_{i}\; -\; n\mu}{\sigma \sqrt{n}} = | ||
| + | \dfrac{1}{\sigma \sqrt{n}} \sum\limits_{i=1}^{n}(x_{i} -\mu) = | ||
| + | \dfrac{1}{\sqrt{n}} \sum\limits_{i=1}^{n}\dfrac{x_{i} -\mu}{\sigma} | ||
| + | = \dfrac{1}{\sqrt{n}} \sum\limits_{i=1}^{n} y_i | ||
| + | </math> | ||
| − | + | ||
| − | <math>\ | + | Jej funkcja charakterystyczna |
| − | + | ||
| − | + | <math>\phi_S(z) = E(e^{izS}) = E\left(e^{iz \frac{1}{\sqrt{n}} \sum\limits_{i=1}^{n} y_i} \right) | |
| + | </math> | ||
<math> | <math> | ||
| − | \ | + | = E\left(\prod_{i=1}^{n} e^{iz \frac{1}{\sqrt{n}} y_i} \right) |
| − | (z | + | </math> |
| + | |||
| + | ponieważ zmienne <math>y_i</math> są wzajemnie niezależne, | ||
| + | |||
| + | <math>\phi_S(z)= \prod_{i=1}^{n} E\left( e^{i\frac{z}{\sqrt{n}} y_i } \right) | ||
| + | = \prod_{i=1}^{n} \phi_{y_i}\left(\frac{z}{\sqrt{n}}\right) | ||
| + | </math> | ||
| + | |||
| + | ponieważ zmienne <math>y_i</math> pochodzą z tego samego rozkładu prawdopodobieństwa, | ||
| + | |||
| + | <math>\phi_S(z)= | ||
| + | \prod_{i=1}^{n} \phi_{y_i}\left(\frac{z}{\sqrt{n}}\right) = | ||
| + | \left( \phi_{y_i}\left(\frac{z}{\sqrt{n}}\right) \right)^n = | ||
| + | \left( 1-\frac{(z/\sqrt{n})^{2}}{2}+\cdots \right)^n = | ||
| + | \left( 1-\frac{z^2}{2n}+\cdots \right)^n | ||
</math> | </math> | ||
| − | + | ||
| − | + | ||
| + | Przy przejściu z <math>n</math> do nieskończoności (i pomijaniu wyrazów rzędu wyższego niż drugi) dostajemy | ||
<center><math> | <center><math> | ||
| − | + | \phi_y(z)\rightarrow | |
| + | \underset{n\rightarrow \infty }{\lim }\left(1-\frac{z^2}{2n}\right)^n= | ||
| + | e^{\frac{-z^{2}}{2}} | ||
</math></center> | </math></center> | ||
| − | + | ||
| − | + | bo | |
| − | + | <math>e^x=\lim_{n\rightarrow\infty} (1+x/n)^n</math> | |
| − | + | ||
| + | Pozostaje pokazać, że jest to postać funkcji charakterystycznej rozkładu Gaussa. | ||
| + | |||
| + | ====Transformata Fouriera funkcji Gaussa==== | ||
| + | Funkcja charakterystyczna rozkładu normalnego o wartości oczekiwanej 0 i jednostkowej wariancji będzie miała postać | ||
| + | |||
| + | <math> | ||
| + | \phi _{x}(t)= | ||
| + | \int\limits_{-\infty}^\infty e^{itx}\frac{1}{\sqrt{2\pi }} e^{\frac{-x^{2}}{2}} dx = | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \left( \cos(tx) + i \sin(tx) \right) e^{\frac{-x^2}{2}} dx = | ||
| + | </math> | ||
| + | |||
<math> | <math> | ||
| − | \ | + | \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \cos(tx) e^{\frac{-x^2}{2}} dx + |
| + | \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty i \sin(tx) e^{\frac{-x^2}{2}} dx | ||
</math> | </math> | ||
| − | |||
| − | + | ponieważ funkcja <math>\sin(x)</math> jest antysymetryczna, druga całka znika. Dostajemy | |
| − | |||
| − | |||
<math> | <math> | ||
| − | \ | + | \int\limits_{-\infty}^\infty e^{itx}\frac{1}{\sqrt{2\pi }} e^{\frac{-x^2}{2}} dx = |
| + | \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \cos(tx) e^{\frac{-x^2}{2}} dx | ||
</math> | </math> | ||
| − | + | Dla części symetrycznej znajdujemy w tablicach całkę oznaczoną | |
| − | <math> | + | |
| + | <math> | ||
| + | \int\limits_{0}^{\infty} e^{-a^2 x^2} \cos(b x) dx | ||
| + | = | ||
| + | \frac{ \sqrt{\pi} e^{-\tfrac{b^2}{4a^2}} } {2 a} | ||
| + | </math> | ||
| + | |||
| + | po wymnożeniu przez 2 i podstawieniu <math> b=t</math> i <math>a^2=\frac{1}{2}</math> dostajemy | ||
| + | |||
| + | <math> | ||
| + | \int\limits_{-\infty}^{\infty} e^{-\frac{1}{2} x^2} \cos(t x) dx | ||
| + | = | ||
| + | \frac{ \sqrt{\pi} e^{ -\frac{t^2} { 4 \frac{1}{2} } } } {\frac{1}{\sqrt{2}}} | ||
| + | = | ||
| + | \sqrt{2\pi} e^{-\frac{t^2}{2}} | ||
| + | </math> , czyli | ||
| + | |||
| + | |||
<center><math> | <center><math> | ||
| − | \ | + | \phi _{x}(t) = |
| + | \int\limits_{-\infty}^\infty e^{itx}\frac{1}{\sqrt{2\pi }} e^{\frac{-x^{2}}{2}} dx = | ||
| + | e^{-t^2 / 2} | ||
| + | </math></center> | ||
| + | |||
| + | |||
| + | |||
| + | W analizie sygnałów wynik ten będzie oznaczał, że transformacja Fouriera funkcji Gaussa jest funkcją Gaussa. W tym konkretnym przypadku otrzymaliśmy funkcję tożsamą z funkcją charakterystyczną rozkładu rozważanej sumy zmiennych, czyli rozkład ten będzie (w przypadku granicznym) miał postać funkcji Gaussa. | ||
| − | |||
| − | |||
| − | |||
| − | |||
[[Plik:Ctg.png|300px|thumb|left|<figure id="fig:ctg"></figure>Ilustracja działania Centralnego Twierdzenia Granicznego. Zmienną | [[Plik:Ctg.png|300px|thumb|left|<figure id="fig:ctg"></figure>Ilustracja działania Centralnego Twierdzenia Granicznego. Zmienną | ||
<math>x_i</math> bierzemy z rozkładu równomiernego, kolejne histogramy przedstawiają sumę 2, 3 i 4 | <math>x_i</math> bierzemy z rozkładu równomiernego, kolejne histogramy przedstawiają sumę 2, 3 i 4 | ||
| − | zmiennych <math>x_i</math> dla | + | zmiennych <math>x_i</math> dla 10 000 losowań. Widać dużą zgodność z dopasowanym rozkładem |
normalnym (ciągła linia) już dla niewielu sumowanych zmiennych. | normalnym (ciągła linia) już dla niewielu sumowanych zmiennych. | ||
]] | ]] | ||
| Linia 130: | Linia 275: | ||
przypadku sumy zmiennych pochodzących z rozkładu równomiernego. Jak | przypadku sumy zmiennych pochodzących z rozkładu równomiernego. Jak | ||
widać, już dla sumy 3 zmiennych rozkład wydaje się bardzo podobny do | widać, już dla sumy 3 zmiennych rozkład wydaje się bardzo podobny do | ||
| − | normalnego. Niestety, często istotne bywają różnice | + | normalnego. Niestety, często istotne bywają różnice dla wartości bardzo dużych lub bardzo małych. Otóż według |
| − | + | [[WnioskowanieStatystyczne/Rozklady-przyklady#label-eq:78|wzoru]] wartości gęstości | |
| − | [[WnioskowanieStatystyczne/ | ||
prawdopodobieństwa rozkładu normalnego dążą do zera dla dużych | prawdopodobieństwa rozkładu normalnego dążą do zera dla dużych | ||
wartości bezwzględnych zmiennej asymptotycznie, lecz zera faktycznie | wartości bezwzględnych zmiennej asymptotycznie, lecz zera faktycznie | ||
Aktualna wersja na dzień 14:10, 18 mar 2024
Wnioskowanie_Statystyczne_-_wykład
Spis treści
Rozkład Gaussa
Rozkład Gaussa (zwany też rozkładem normalnym lub krzywą dzwonową) zależy od parametrów [math]\mu[/math] i [math]\sigma[/math]. Jego gęstość prawdopodobieństwa określona jest wzorem:
Parametry te są tak dobrane, że wartość oczekiwana wynosi [math]\mu[/math], a wariancja [math]\sigma^2[/math].
Rozkład Gaussa dla zerowej wartości oczekiwanej i jednostkowej wariancji ([math]\mu=0, \sigma^2=1[/math]) zwiemy standardowym rozkładem Gaussa i oznaczamy zwykle [math]N(0,1)[/math]. Na wykresie zaznaczono na nim m. in. wartość całki od [math]-\infty[/math] do [math]-1[/math], czyli prawdopodobieństwo, że wylosowana z tego rozkładu liczba będzie mniejsza niż [math]-1[/math]. Jak widać, wynosi ono ok. 16%, a jeśli weźmiemy pod uwagę również wartości większe od 1, będzie to aż 32%! Oznacza to, że przy losowaniu wielu liczb z tego rozkładu niemal 1/3 wyników może znaleźć się w odległości większej niż [math]\sigma[/math] od wartości oczekiwanej.
Rozkład Gaussa pełni w statystyce bardzo znaczącą rolę ze względu na Centralne Twierdzenie Graniczne, mówiące o asysmptotycznym rozkładzie sumy dużej liczby niezależnych zmiennych losowych, których rozkłady spełniają pewne warunki. Udowodnimy je w najprostszym przypadku, kiedy wszystkie te zmienne pochodzą z tego samego rozkładu gęstości prawdopodobieństwa. Na potrzeby tego dowodu musimy najpierw wprowadzić pojęcie funkcji charakterystycznej.
Funkcja charakterystyczna rozkładu prawdopodobieństwa
Dla zmiennej losowej [math]x[/math] jest to wartość oczekiwana wyrażenia [math]e^{itx}[/math], gdzie [math]i=\sqrt{-1}[/math]. Dla rozkładów ciągłych jest to transformata Fouriera funkcji gęstości prawdopodobieństwa [math]f(x)[/math]:
Użyteczne będą poniższe związki, które wyprowadzić można bezpośrednio z definicji:
Funkcja charakterystyczna rozkładu sumy zmiennych niezależnych
Dla niezależnych zmiennych [math]x[/math] i [math]y[/math]:
[math] w=x+y\Rightarrow \phi _{w}(t) =\phi _{x}\left( t\right) \cdot \phi_{y}(t). [/math]
Dowód:
[math] \phi _{w}(t) = E(e^{it(x+y)})=E(e^{itx}\cdot e^{ity}) = E(e^{itx})\cdot E(e^{ity})=\phi _{x}\left( t\right) \cdot \phi_{y}(t). [/math]
Pochodna funkcji charakterystycznej
Bezpośrednio z definicji (różniczkujemy po [math]dt[/math], więc przy każdym różniczkowaniu spada nam z wykładnika [math]i x[/math], [math]x[/math] zostaje pod całką a [math]i[/math] jako stała wychodzi przed całkę) widać, że:
Związek pochodnej funkcji charakterystycznej z momentami zmiennej losowej
[math]n[/math]-ta pochodna funkcji charakterystycznej w zerze (czyli dla [math]t=0[/math]) wynosi
Twierdzenie Lindeberga–Lévy'ego
Zakładamy, że [math]x_{i}[/math] są niezależnymi zmiennymi podlegającymi (dowolnemu) rozkładowi o skończonej wartości oczekiwanej [math]\mu[/math] i wariancji [math]\sigma^{2}[/math], czyli wszystkie sumowane zmienne [math]x_i[/math] pochodzą z tego samego rozkładu prawdopodobieństwa, o którym nie zakładamy nic ponad to, że ma skończone [math]\mu[/math] i [math]\sigma[/math]. Wielkość
dla [math]n\rightarrow \infty[/math] zbiega do rozkładu normalnego o zerowej wartości średniej i jednostkowej wariancji.
Dowód twierdzenia Lindeberga–Lévy'ego
Rozważmy zmienną [math]y_i[/math] o zerowej wartości oczekiwanej i jednostkowej wariancji
Funkcję charakterystyczną rozkładu zmiennej [math]y_i[/math]
możemy rozwinąć w szereg Taylora wokół [math]z=0[/math]
Z wyprowadzonej wcześniej własności funkcji charakterystycznej (4) [math] \phi^{(n)}(0)= i^{n}E(x^{n}) [/math] wynika, że
[math]\phi_{y_i}^{(0)}(0)=1[/math],
[math]\phi_{y_i}^{(1)}(0)=0[/math] (wartość oczekiwana),
[math]\phi_{y_i}^{(2)}(0)=-1[/math] ([math]i^2[/math] * wariancja),
czyli funkcja charakterystyczna zmiennej [math]y_i[/math] rozwinięta w szereg Taylora (6) do wyrazów drugiego rzędu będzie miała postać
Wrócmy do występującej w twierdzeniu sumy [math]S[/math]
[math] S=\dfrac{ \sum\limits_{i=1}^{n}x_{i}\; -\; n\mu}{\sigma \sqrt{n}} = \dfrac{1}{\sigma \sqrt{n}} \sum\limits_{i=1}^{n}(x_{i} -\mu) = \dfrac{1}{\sqrt{n}} \sum\limits_{i=1}^{n}\dfrac{x_{i} -\mu}{\sigma} = \dfrac{1}{\sqrt{n}} \sum\limits_{i=1}^{n} y_i [/math]
Jej funkcja charakterystyczna
[math]\phi_S(z) = E(e^{izS}) = E\left(e^{iz \frac{1}{\sqrt{n}} \sum\limits_{i=1}^{n} y_i} \right) [/math] [math] = E\left(\prod_{i=1}^{n} e^{iz \frac{1}{\sqrt{n}} y_i} \right) [/math]
ponieważ zmienne [math]y_i[/math] są wzajemnie niezależne,
[math]\phi_S(z)= \prod_{i=1}^{n} E\left( e^{i\frac{z}{\sqrt{n}} y_i } \right) = \prod_{i=1}^{n} \phi_{y_i}\left(\frac{z}{\sqrt{n}}\right) [/math]
ponieważ zmienne [math]y_i[/math] pochodzą z tego samego rozkładu prawdopodobieństwa,
[math]\phi_S(z)= \prod_{i=1}^{n} \phi_{y_i}\left(\frac{z}{\sqrt{n}}\right) = \left( \phi_{y_i}\left(\frac{z}{\sqrt{n}}\right) \right)^n = \left( 1-\frac{(z/\sqrt{n})^{2}}{2}+\cdots \right)^n = \left( 1-\frac{z^2}{2n}+\cdots \right)^n [/math]
Przy przejściu z [math]n[/math] do nieskończoności (i pomijaniu wyrazów rzędu wyższego niż drugi) dostajemy
bo [math]e^x=\lim_{n\rightarrow\infty} (1+x/n)^n[/math]
Pozostaje pokazać, że jest to postać funkcji charakterystycznej rozkładu Gaussa.
Transformata Fouriera funkcji Gaussa
Funkcja charakterystyczna rozkładu normalnego o wartości oczekiwanej 0 i jednostkowej wariancji będzie miała postać
[math] \phi _{x}(t)= \int\limits_{-\infty}^\infty e^{itx}\frac{1}{\sqrt{2\pi }} e^{\frac{-x^{2}}{2}} dx = [/math]
[math] \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \left( \cos(tx) + i \sin(tx) \right) e^{\frac{-x^2}{2}} dx = [/math]
[math] \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \cos(tx) e^{\frac{-x^2}{2}} dx + \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty i \sin(tx) e^{\frac{-x^2}{2}} dx [/math]
ponieważ funkcja [math]\sin(x)[/math] jest antysymetryczna, druga całka znika. Dostajemy
[math] \int\limits_{-\infty}^\infty e^{itx}\frac{1}{\sqrt{2\pi }} e^{\frac{-x^2}{2}} dx = \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \cos(tx) e^{\frac{-x^2}{2}} dx [/math]
Dla części symetrycznej znajdujemy w tablicach całkę oznaczoną
[math] \int\limits_{0}^{\infty} e^{-a^2 x^2} \cos(b x) dx = \frac{ \sqrt{\pi} e^{-\tfrac{b^2}{4a^2}} } {2 a} [/math]
po wymnożeniu przez 2 i podstawieniu [math] b=t[/math] i [math]a^2=\frac{1}{2}[/math] dostajemy
[math] \int\limits_{-\infty}^{\infty} e^{-\frac{1}{2} x^2} \cos(t x) dx = \frac{ \sqrt{\pi} e^{ -\frac{t^2} { 4 \frac{1}{2} } } } {\frac{1}{\sqrt{2}}} = \sqrt{2\pi} e^{-\frac{t^2}{2}} [/math] , czyli
W analizie sygnałów wynik ten będzie oznaczał, że transformacja Fouriera funkcji Gaussa jest funkcją Gaussa. W tym konkretnym przypadku otrzymaliśmy funkcję tożsamą z funkcją charakterystyczną rozkładu rozważanej sumy zmiennych, czyli rozkład ten będzie (w przypadku granicznym) miał postać funkcji Gaussa.
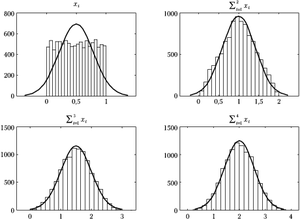
Rysunek 1 ilustruje powyższe twierdzenie dla przypadku sumy zmiennych pochodzących z rozkładu równomiernego. Jak widać, już dla sumy 3 zmiennych rozkład wydaje się bardzo podobny do normalnego. Niestety, często istotne bywają różnice dla wartości bardzo dużych lub bardzo małych. Otóż według wzoru wartości gęstości prawdopodobieństwa rozkładu normalnego dążą do zera dla dużych wartości bezwzględnych zmiennej asymptotycznie, lecz zera faktycznie nie osiągają. Inaczej mówiąc, prawdopodobieństwo wylosowania dowolnie dużej wartości z rozkładu Gaussa będzie małe, ale nie zerowe. Za to suma np. czterech zmiennych z rozkładu równomiernego od zera do jedynki (prawy dolny wykres rys. 1) nie przekroczy nigdy wartości 4, czyli prawdopodobieństwo dla [math]x\gt 4[/math] będzie dokładnie zerem. I choć w skali rysunku 1 efekt ten jest prawie niewidoczny, warto pamiętać, że testy oparte na założeniu normalności rozkładów często operują właśnie w okolicach tych "ogonów", gdzie przybliżenie rozkładu normalnego, uzyskane za pomocą tej prostej procedury, zawodzi.