WnioskowanieStatystyczne/Rozklady: Różnice pomiędzy wersjami
(UWAGA! Usunięcie treści (strona pozostała pusta)!) |
|||
| Linia 1: | Linia 1: | ||
| + | ==Rozkłady prawdopodobieństwa== | ||
| + | Rozkład prawdpopodobieństwa — zgodnie z nazwą — będzie funkcją określającą, | ||
| + | jak prawdopodobieństwo rozkłada się pomiędzy możliwe wyniki danego | ||
| + | doświadczenia. Mieliśmy już z nim do czynienia w pierwszej części książki, | ||
| + | <xr id="fig:boot+mc_kosz">rysunek %i</xr> przypomina niektóre z tych przypadków. | ||
| + | |||
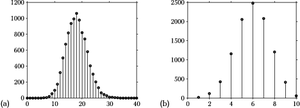
| + | [[Plik:Boot+mc_kosz.png|300px|thumb|left|<figure id="fig:boot+mc_kosz"></figure>(a) rozkład liczby jedynek uzyskany z 10 tysięcy repróbkowań ze | ||
| + | zwracaniem (bootstrap) próby 18 jedynek i 82 zer; | ||
| + | (b) liczba trafień na 10 rzutów do kosza, przy średnim prawdopodobieństwie | ||
| + | trafienia 0,6 ]] | ||
| + | |||
| + | Nie są to prawdopodobieństwa, gdyż nie spełniają [[WnioskowanieStatystyczne/Prawdopodobieństwo#label-eq:45|aksjomatu]] <math>(0\leq P(A)\leq 1)</math>, który wraz z [[WnioskowanieStatystyczne/Prawdopodobieństwo#label-eq:43|aksjomatem]] <math>(P(\Omega)=1)</math> możemy spełnić dzieląc liczbę wystąpień każdego przypadku przez całkowitą liczbę eksperymentów — | ||
| + | wtedy suma wszystkich prawdopodobieństw (czyli <math>P(\Omega)</math>) | ||
| + | wyniesie 1. Przykład tak znormalizowanego dyskretnego rozkładu | ||
| + | prawdopodobieństwa przedstawia rysunek <xr id="fig:dysk_i_plask">rysunek %i(a)</xr>. | ||
| + | |||
| + | Pozostaje jeszcze problem formalny: występujące w klasycznej teorii | ||
| + | funkcje nie są określone na zdarzeniach, tylko na liczbach. Przejście | ||
| + | od zdarzeń do odpowiadających im liczb wymaga pojęcia ''zmiennej | ||
| + | losowej'' – odwzorowania <math>X(.)</math> z przestrzeni zdarzeń do | ||
| + | przestrzeni liczb rzeczywistych. Na przykład w doświadczeniu | ||
| + | polegającym na rzucaniu kostką zmienna losowa przypisze liczbę 4 | ||
| + | przypadkowi, w którym na górnej ściance rzuconej kostki widać cztery | ||
| + | kropki. | ||
| + | |||
| + | Liczby (czyli zmienne losowe) są już pełnoprawnymi argumentami | ||
| + | funkcji, ale z definicją rozkładu prawdopodobieństwa będzie jeszcze | ||
| + | trochę kłopotu, jeśli wyniki eksperymentu będą pochodzić z ciągłych | ||
| + | przedziałów zmiennej losowej, a nie, jak w przykładach z rysunku <xr id="fig:boot+mc_kosz">rysunek %i</xr>, ze zbioru dyskretnego. | ||
| + | |||
| + | ==Rozkłady ciągłe — gęstość prawdopodobieństwa== | ||
| + | |||
| + | [[Plik:Rozklad_dyskretny_i_plaski.png|300px|thumb|left|<figure | ||
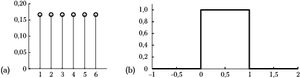
| + | id="fig:dysk_i_plask"></figure>(a) dyskretny rozkład prawdopodobieństw | ||
| + | wyników rzutu kostką; (b) ciągły rozkład prawdopodobieństwa dla liczb | ||
| + | rzeczywistych z przedziału od zera do jednego. ]] | ||
| + | |||
| + | Z rozkładem ciągłym mieliśmy do czynienia, gdy używaliśmy generatora | ||
| + | liczb losowych — losował on z równym prawdopodobieństwem liczby | ||
| + | rzeczywiste z przedziału od zera do jednego. Funkcja przypisująca | ||
| + | równe prawdopodobieństwa liczbom od zera do jednego powinna wyglądać | ||
| + | jak na <xr id="fig:dysk_i_plask">rysunku %i(b)</xr>. A jednak coś się | ||
| + | tu nie zgadza... | ||
| + | |||
| + | Zacznijmy od rozkładu dyskretnego, czyli <xr | ||
| + | id="fig:dysk_i_plask">wykresu %i(a)</xr>. Prawdopodobieństwo dla | ||
| + | zmiennej losowej (teraz nie jest to już formalnie zdarzenie) | ||
| + | wynoszącej na przykład 2 odczytujemy jako wynoszące 0,167. Czyli | ||
| + | mniejsze od 1 i większe od zera. Suma prawdopodobieństw dla wszystkich | ||
| + | możliwych wartości zmiennej losowej wyniesie 1 — wszystko zgadza się | ||
| + | z [[WnioskowanieStatystyczne/Prawdopodobieństwo#Częstościowa definicja prawdopodobieństwa|aksjomatami definicji prawdopodobieństwa]]. | ||
| + | |||
| + | Teraz spróbujmy z wykresu po prawej stronie odczytać wartość | ||
| + | prawdopodobieństwa wylosowania jakiejś liczby spomiędzy 0 i 1. Jeden? | ||
| + | To oznacza pewność — niemożliwe. Na osi <math>y</math> powinna | ||
| + | występować jakaś znacznie mniejsza wartość... Ale jaka? | ||
| + | |||
| + | Zastanówmy się: niezależnie od tego, jak małą (niezerową i nieujemną) | ||
| + | wartość przyjmiemy dla prawdopodobieństwa wylosowania dowolnej liczby | ||
| + | z tego przedziału, to gdy zaczniemy je sumować dla wszystkich | ||
| + | możliwych wyników, których na odcinku <math>(0, 1)</math> jest wszak | ||
| + | nieskończenie wiele, zawsze dostaniemy więcej niż jeden. Najwyraźniej | ||
| + | tak się nie da. | ||
| + | |||
| + | Widać już, że sumę będziemy musieli zastąpić całką — jest to właśnie | ||
| + | graniczny przypadek sumy. W tym układzie aksjomat | ||
| + | <math>P(\Omega)=1</math>, który dla przypadku dyskretnego wyrażał się | ||
| + | sumą | ||
| + | |||
| + | <math> | ||
| + | \sum_i P(X=x_i) = 1, | ||
| + | </math> | ||
| + | |||
| + | teraz będzie wyrażał się całką | ||
| + | |||
| + | <math> | ||
| + | \int p(x) dx = 1, | ||
| + | </math> | ||
| + | |||
| + | gdzie prawdopodobieństwo <math>P</math> zastąpiła, z przyczyn, które | ||
| + | staną się jasne za chwilę, gęstość prawdopodobieństwa <math>p</math>. | ||
| + | Łatwo sprawdzić, że całka rozkładu z <xr | ||
| + | id="fig:dysk_i_plask">rys. %i</xr> spełnia ten warunek. Jednak | ||
| + | pozostaje problem odczytywania wartości prawdopodobieństwa dla | ||
| + | konkretnej wartości zmiennej losowej. | ||
| + | |||
| + | Przypomnijmy sobie, że [[WnioskowanieStatystyczne/Bootstrap|symulując rzuty monetą]] korzystaliśmy z faktu, że prawdopodobieństwo wylosowania liczby | ||
| + | mniejszej niż <math>\frac1 2</math> wynosi 0,5. Zdefiniujmy więc | ||
| + | ''dystrybuantę'' prawdopodobieństwa zmiennej losowej <math>X</math> | ||
| + | jako prawdopodobieństwo wystąpienia któregokolwiek ze zdarzeń, dla | ||
| + | których zmienna losowa przyjmuje wartości mniejsze od <math>x</math>: | ||
| + | |||
| + | <equation id="eq:59"> | ||
| + | <math> | ||
| + | F(x)=P[X \leq x]. | ||
| + | </math> | ||
| + | </equation> | ||
| + | |||
| + | Będzie to oczywiście funkcja niemalejąca, dążąca do zera dla małych | ||
| + | <math>x</math> i do jednego dla dużych. Dla rozkładu z <xr | ||
| + | id="fig:dysk_i_plask">rysunku %i</xr>(b) dystrybuanta będzie wyglądać | ||
| + | jak na <xr id="fig:plaski">rysunku %i</xr>. | ||
| + | |||
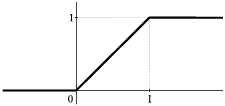
| + | [[Plik:Dystryb_plaski.png|300px|thumb|left|<figure | ||
| + | id="fig:plaski"></figure>Dystrybuanta ciągłej zmiennej losowej o | ||
| + | równym prawdopodobieństwie na przedziale (0, 1).]] | ||
| + | |||
| + | Dopiero teraz '''gęstość prawdopodobieństwa''' zmiennej losowej określimy jako | ||
| + | pochodną dystrybuanty | ||
| + | |||
| + | <equation id="eq:59"> | ||
| + | <math> | ||
| + | p(x)=\frac{d F(x)}{dx}=\frac{P[x\leq X\leq x+dx]}{dx}. | ||
| + | </math> | ||
| + | </equation> | ||
| + | |||
| + | Dlaczego gęstość, a nie po prostu rozkład prawdopodobieństwa, jak w | ||
| + | przypadku dyskretnym? Właśnie ze względu na problemy z odczytem | ||
| + | prawdopodobieństwa dla konkretnej wartości zmiennej. Na podobny | ||
| + | problem trafiamy np. w fizyce, próbując obliczyć masę punktu. Masa to | ||
| + | iloczyn (całka) gęstości i objętości, a punkt ma zerową objętość. Aby | ||
| + | otrzymać niezerową masę, gęstość materii musimy scałkować w jakimś | ||
| + | niezerowym obszarze — nie można przyjąć za masę gęstości materii w | ||
| + | danym punkcie. Tak samo w przypadku ciągłych rozkładów gęstości | ||
| + | prawdopodobieństwa, prawdopodobieństwo możemy obliczyć tylko dla | ||
| + | niezerowego przedziału zmiennej losowej, a wartość odczytywaną dla | ||
| + | konkretnej wartości zmiennej losowej interpretujemy jako gęstość. | ||
Wersja z 13:40, 22 maj 2015
Rozkłady prawdopodobieństwa
Rozkład prawdpopodobieństwa — zgodnie z nazwą — będzie funkcją określającą, jak prawdopodobieństwo rozkłada się pomiędzy możliwe wyniki danego doświadczenia. Mieliśmy już z nim do czynienia w pierwszej części książki, rysunek 1 przypomina niektóre z tych przypadków.
Nie są to prawdopodobieństwa, gdyż nie spełniają aksjomatu [math](0\leq P(A)\leq 1)[/math], który wraz z aksjomatem [math](P(\Omega)=1)[/math] możemy spełnić dzieląc liczbę wystąpień każdego przypadku przez całkowitą liczbę eksperymentów — wtedy suma wszystkich prawdopodobieństw (czyli [math]P(\Omega)[/math]) wyniesie 1. Przykład tak znormalizowanego dyskretnego rozkładu prawdopodobieństwa przedstawia rysunek rysunek 2(a).
Pozostaje jeszcze problem formalny: występujące w klasycznej teorii funkcje nie są określone na zdarzeniach, tylko na liczbach. Przejście od zdarzeń do odpowiadających im liczb wymaga pojęcia zmiennej losowej – odwzorowania [math]X(.)[/math] z przestrzeni zdarzeń do przestrzeni liczb rzeczywistych. Na przykład w doświadczeniu polegającym na rzucaniu kostką zmienna losowa przypisze liczbę 4 przypadkowi, w którym na górnej ściance rzuconej kostki widać cztery kropki.
Liczby (czyli zmienne losowe) są już pełnoprawnymi argumentami funkcji, ale z definicją rozkładu prawdopodobieństwa będzie jeszcze trochę kłopotu, jeśli wyniki eksperymentu będą pochodzić z ciągłych przedziałów zmiennej losowej, a nie, jak w przykładach z rysunku rysunek 1, ze zbioru dyskretnego.
Rozkłady ciągłe — gęstość prawdopodobieństwa
Z rozkładem ciągłym mieliśmy do czynienia, gdy używaliśmy generatora liczb losowych — losował on z równym prawdopodobieństwem liczby rzeczywiste z przedziału od zera do jednego. Funkcja przypisująca równe prawdopodobieństwa liczbom od zera do jednego powinna wyglądać jak na rysunku 2(b). A jednak coś się tu nie zgadza...
Zacznijmy od rozkładu dyskretnego, czyli wykresu 2(a). Prawdopodobieństwo dla zmiennej losowej (teraz nie jest to już formalnie zdarzenie) wynoszącej na przykład 2 odczytujemy jako wynoszące 0,167. Czyli mniejsze od 1 i większe od zera. Suma prawdopodobieństw dla wszystkich możliwych wartości zmiennej losowej wyniesie 1 — wszystko zgadza się z aksjomatami definicji prawdopodobieństwa.
Teraz spróbujmy z wykresu po prawej stronie odczytać wartość prawdopodobieństwa wylosowania jakiejś liczby spomiędzy 0 i 1. Jeden? To oznacza pewność — niemożliwe. Na osi [math]y[/math] powinna występować jakaś znacznie mniejsza wartość... Ale jaka?
Zastanówmy się: niezależnie od tego, jak małą (niezerową i nieujemną) wartość przyjmiemy dla prawdopodobieństwa wylosowania dowolnej liczby z tego przedziału, to gdy zaczniemy je sumować dla wszystkich możliwych wyników, których na odcinku [math](0, 1)[/math] jest wszak nieskończenie wiele, zawsze dostaniemy więcej niż jeden. Najwyraźniej tak się nie da.
Widać już, że sumę będziemy musieli zastąpić całką — jest to właśnie graniczny przypadek sumy. W tym układzie aksjomat [math]P(\Omega)=1[/math], który dla przypadku dyskretnego wyrażał się sumą
[math] \sum_i P(X=x_i) = 1, [/math]
teraz będzie wyrażał się całką
[math] \int p(x) dx = 1, [/math]
gdzie prawdopodobieństwo [math]P[/math] zastąpiła, z przyczyn, które staną się jasne za chwilę, gęstość prawdopodobieństwa [math]p[/math]. Łatwo sprawdzić, że całka rozkładu z rys. 2 spełnia ten warunek. Jednak pozostaje problem odczytywania wartości prawdopodobieństwa dla konkretnej wartości zmiennej losowej.
Przypomnijmy sobie, że symulując rzuty monetą korzystaliśmy z faktu, że prawdopodobieństwo wylosowania liczby mniejszej niż [math]\frac1 2[/math] wynosi 0,5. Zdefiniujmy więc dystrybuantę prawdopodobieństwa zmiennej losowej [math]X[/math] jako prawdopodobieństwo wystąpienia któregokolwiek ze zdarzeń, dla których zmienna losowa przyjmuje wartości mniejsze od [math]x[/math]:
Będzie to oczywiście funkcja niemalejąca, dążąca do zera dla małych [math]x[/math] i do jednego dla dużych. Dla rozkładu z rysunku 2(b) dystrybuanta będzie wyglądać jak na rysunku 3.
Dopiero teraz gęstość prawdopodobieństwa zmiennej losowej określimy jako pochodną dystrybuanty
Dlaczego gęstość, a nie po prostu rozkład prawdopodobieństwa, jak w przypadku dyskretnym? Właśnie ze względu na problemy z odczytem prawdopodobieństwa dla konkretnej wartości zmiennej. Na podobny problem trafiamy np. w fizyce, próbując obliczyć masę punktu. Masa to iloczyn (całka) gęstości i objętości, a punkt ma zerową objętość. Aby otrzymać niezerową masę, gęstość materii musimy scałkować w jakimś niezerowym obszarze — nie można przyjąć za masę gęstości materii w danym punkcie. Tak samo w przypadku ciągłych rozkładów gęstości prawdopodobieństwa, prawdopodobieństwo możemy obliczyć tylko dla niezerowego przedziału zmiennej losowej, a wartość odczytywaną dla konkretnej wartości zmiennej losowej interpretujemy jako gęstość.