|
|
| (Nie pokazano 22 pośrednich wersji utworzonych przez tego samego użytkownika) |
| Linia 1: |
Linia 1: |
| − | ==Sygnał==
| + | Sygnały zapisujemy, przetwarzamy i analizujemy w postaci ciągów liczb. Przejście od sygnału ciągłego do cyfrowego odbywa się przez proces próbkowania, czyli zapisywania kolejnych amplitud sygnału w ustalonych, stałych odstępach czasu, [[TI/Cyfrowy_świat|omawiany wcześniej na TIiK]]. |
| − | W języku potocznym sygnał to [http://sjp.pwn.pl/lista.php?co=sygnał|''wszelki umowny znak o treści informacyjnej'']. Z kolei w ramach tego wykładu przez
| |
| − | ''sygnał'' rozumieć będziemy funkcję (zależną zwykle od
| |
| − | czasu<ref>Uzyskane rezultaty nie zależą od fizycznej postaci
| |
| − | zmiennej zależnej (<math>t</math>) i większość z nich stosowana jest np. w
| |
| − | analizie obrazów. </ref>) <math>s(t)</math>. Czy mówimy o tym samym?
| |
| | | | |
| − | Rozważmy przykładowe znaki umowne: czerwone światło na
| + | [[Plik:AD.png|150px|bezramki]] |
| − | skrzyżowaniu to docierająca do naszych oczu fala
| |
| − | elektromagnetyczna o długości ok. 0,0000007 metra;
| |
| − | znaczeniem tego sygnału jest "stój". Litery, które czytasz, to
| |
| − | pewien rozkład zaczernienia kartki, dający się niewątpliwie opisać
| |
| − | z pomocą funkcji matematycznych, gdyż w tej właśnie formie
| |
| − | przechodził kolejne etapy poprzedzające druk. Ich znaczenie...
| |
| | | | |
| − | Wydaje się, że fizyczną postać informacji — umożliwiającą jej przekaz
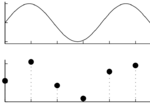
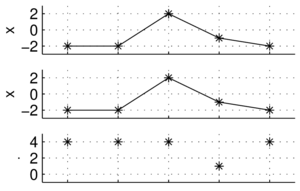
| + | Ciągły sygnał z górnego rysunku, po próbkowaniu w punktach symbolizowanych czarnymi kropkami na rysunku dolnym, na dysku zostaje zapisany jako ciąg liczb: |
| − | czy przechowywanie — można nazwać sygnałem. A odwrotnie? Czy każdy
| |
| − | sygnał niesie ze sobą jakąś informację? Owszem, tylko niekiedy może | |
| − | ona być nieskończenie trudna do odczytania (dokładam wszelkich starań,
| |
| − | aby nie miało to miejsca w przypadku tego tekstu :-). A sygnały zupełnie
| |
| − | przypadkowe? Okazuje się, że nie są wcale powszechne ani łatwe do
| |
| − | wytworzenia <ref>Za sygnał przypadkowy możemy uznać sekwencję
| |
| − | liczb, przyjmującym wartości z określonego przedziału, np. od 0 do 1, | |
| − | z jednakowym prawdopodobieństwem. Ponadto w takiej sekwencji nie
| |
| − | powinny występować ''żadne'' zależności między prawdopodobieństwem
| |
| − | "wylosowania" następnej liczby a wartościami poprzednich, gdyż w
| |
| − | nich właśnie może być zakodowana informacja. W przyrodzie znamiona
| |
| − | takiej przypadkowości noszą zjawiska związane z rozpadem
| |
| − | promieniotwórczym.</ref>, więc właśnie całkowitą przypadkowość można uznać
| |
| − | za niesioną przez sygnał informację.
| |
| | | | |
| − | ==Analiza==
| + | 102, 195, 80, 16, 147, 178 |
| − | Informację niesioną przez milion liczb, wylosowanych niezależnie
| |
| − | spomiędzy 0 i 1, można przedstawić krócej niż przez wyliczenie ich
| |
| − | wszystkich — choćby tym właśnie zdaniem. Opis ten jest nie tylko
| |
| − | bardziej zwięzły niż przytaczanie miliona wartości, ale oddaje
| |
| − | jednocześnie najważniejsze ich cechy — ''istotę''
| |
| − | sygnału. Zwięzłych, trafny i kompletny opis sygnałów występujących w
| |
| − | przyrodzie to właśnie Święty Graal analizy sygnałów. Ta książka to
| |
| − | zaledwie zbiór wskazówek, które przy rozsądnym stosowaniu mogą nas
| |
| − | czasem doprowadzić w jego pobliże.
| |
| | | | |
| − | Zastanówmy się więc, na czym właściwie ma polegać analiza czy opis
| + | Żeby odtworzyć fizyczne własności sygnału, czyli narysować zapisane wartości próbek (czarne kropki) w odpowiedniej skali, musimy znać ''częstość próbkowania'' i ''stałą kalibracji''. |
| − | sygnału, w przypadku bardziej skomplikowanym niż przytoczony powyżej? | |
| − | Sięgniemy raz jeszcze do [http://sjp.pwn.pl/|''Słownika języka polskiego'']:
| |
| | | | |
| − | '''analiza''' 1. myślowe, pojęciowe wyodrębnienie cech, | + | Wyrażana w hercach (Hz) częstość próbkowania (ang. ''sampling frequency'', <math>f_s</math>) to liczba próbek na sekundę. Jest ona odwrotnością odstępu w czasie między kolejnymi próbkami (<math>\Delta t</math>): |
| − | części, lub składników badanego zjawiska lub przedmiotu; badanie cech
| + | <div align = "center> |
| − | elementów lub struktury czegoś oraz zachodzących między nimi związków
| + | <math>f_s = \dfrac{1}{\Delta t}</math> |
| − | (...)
| + | </div> |
| | | | |
| − | Skoncentrujmy się najpierw na "wyodrębnianiu części lub składników".
| + | Stała kalibracji to współczynnik, przez który mnożymy zapisane liczby, żeby otrzymać wartości w jednostkach fizycznych, na przykład mikrowoltach. |
| − | Ilustrację tego podejścia stanowi rysunek <xr id="fig:1"> %i</xr>.
| |
| | | | |
| − | [[Plik:wstep_rys_1.jpg|thumb|center|600px|alt=Sumowanie sygnałów|<figure id="fig:1"></figure> (a) = (b) + (c) + (d)<br/>(b)=<math> 0.3 \sin(2\pi 12 t)</math> (sinus)<br/>(c)=<math> 0.7 e^{{-(t-0.8)^2}/{0.2}} \sin(2\pi 20 t)</math> (funkcja Gabora)<br/> (d)=<math>0.5 \sin(2\pi\,2\, t\; t )</math> (chirp)]] | + | Oczywiście musimy też wiedzieć, w jakim formacie zapisano na dysku liczby (omawiany rok temu na wykładzie o [[TI/Zera_i_jedynki|binarnych reprezentacjach liczb]]), oraz, w przypadku sygnałów wielozmiennych o jednolitym próbkowaniu, znać liczbę kanałów. Taka dodatkowa informacja (metainformacja) jest konieczna do poprawnego wyświetlenia danych z pliku. |
| | | | |
| − | "Tajemnicę" konstrukcji sygnału z górnej części rysunku
| + | ===Aliasing=== |
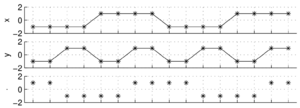
| − | <xr id="fig:1"> %i</xr> odkrywają wyrysowane pod nim funkcje składowe. Sygnał | + | Poza znajomością zależności między zapisanymi liczbami a jednostkami fizycznymi w procesie próbkowania kluczową rolę odgrywa twierdzenie o próbkowaniu (inaczej twierdzenie Nyquista-Shannona, czasem w skrócie twierdzenie Nyquista). Mówi ono, że sygnał ciągły możemy odtworzyć za zapisanych próbek, jeśli częstość próbkowania <math>f_p</math> była wyższa niż dwukrotność najwyższej z występujących w sygnale częstości <math>f_{max}</math>, nazywana częstością Nyquista <math>f_N</math>: |
| − | (a) jest ich (liniową) sumą. Taki przypadek sygnału będącego liniową
| + | <div align = "center> |
| − | kombinacją znanych funkcji możemy przedstawić ogólnie jako
| + | <math> f_s = \dfrac{1}{\Delta t} > 2* f_{max} = f_N</math> |
| | + | </div> |
| | + | Jeśli częstość próbkowania nie była wystarczająco wysoka, nie tylko stracimy informację o zmianach amplitudy sygnału "pomiędzy próbkami", ale dojdzie też do zafałszowania sygnału w niższych częstościach, które z pozoru nie powinny być zaburzone. Efekt ten jest bliżej omówiony w rozdziale [[Aliasing]]. |
| | | | |
| − | <equation id="eq:suma_syg">
| + | [[Plik:Nyquist1.png|600px|bezramki]] |
| − | <math>
| |
| − | s(t) = \sum_{k} \alpha_k g_k
| |
| − | </math>
| |
| − | </equation>
| |
| | | | |
| − | gdzie <math>\{g_i\}</math> to zbiór "znanych" funkcji, a <math>\alpha_i</math> to
| + | ===Sygnał dyskretny jako wektor=== |
| − | współczynniki określające ich wkłady. W konkretnym przypadku sygnału z
| |
| − | rysunku <xr id="fig:1"> %i</xr> wyglądałyby one następująco:
| |
| − | <equation id="eq:zlozenie_sygnalow">
| |
| − | <math>
| |
| − | \left \{
| |
| − | \begin{matrix}
| |
| − | \alpha_1 = 0.3, & g_1 = \sin(2 \pi 12 t)\\
| |
| − | \alpha_2 = 0.7, &g_2 = e^{{-(t-0.8)^2}/{0.2}} \sin(2\pi 20 t)\\
| |
| − | \alpha_3 = 0.5, &g_3 = \sin(2\pi\,2\, t\; t )
| |
| − | \end{matrix}
| |
| − | \right .
| |
| − | </math>
| |
| − | </equation>
| |
| | | | |
| − | Załóżmy, że interesująca nas w sygnale informacja została faktycznie
| + | [https://en.wikipedia.org/wiki/Energy_(signal_processing) Energia sygnału] |
| − | zakodowana według równania <xr id="eq:suma_syg">(%i)</xr>. Niestety, dokładne
| |
| − | "odgadnięcie" reprezentacji typu równania <xr id="eq:zlozenie_sygnalow">(%i)</xr> jest
| |
| − | w ogólnym przypadku — czyli w braku pewnej wiedzy a priori o sygnale
| |
| − | — niemożliwe. Już sam wybór ''rodzaju'' funkcji (np. sinusy i
| |
| − | kosinusy) jest nieskończenie trudny — wszak różnych funkcji jest
| |
| − | nieskończenie wiele! Nawet gdy już zdecydujemy, jakiego rodzaju
| |
| − | funkcje powinny najlepiej opisywać analizowany sygnał, to dobranie ich
| |
| − | parametrów wciąż pozostaje poważnym problemem (patrz np. rozdział [[Reprezentacje_przybliżone#Przybliżenia_adaptacyjne(adaptive_approximations)|o algorytmie Matching Pursuit]]).
| |
| | | | |
| | | | |
| − | Ale analiza to również "badanie cech elementów lub struktury (...)
| + | [[Plik:Product1.png|bezramki]] |
| − | oraz zachodzących między nimi związków". Możemy pokusić się o
| |
| − | ustalenie związku między wartością sygnału w danej chwili i w chwilach
| |
| − | poprzednich, w postaci zależności liniowej -- takie założenie realizuje [[Klasyczna#Model_AR|opisany w jednym z następnych rozdziałów model AR]]:
| |
| | | | |
| − | <equation id="eq:zal_lin">
| + | [[Plik:Product2.png|bezramki]] |
| − | <math>
| |
| − | s(t) = \alpha_1 s(t - \Delta t) + \alpha_2 s(t -2\Delta t) + \alpha_3 s(t - 3 \Delta t) + ...
| |
| − | </math>
| |
| − | </equation>
| |
| | | | |
| − | Jeśli weźmiemy pod uwagę czynniki przypadkowe, jak np. niedokładność
| + | [[Plik:Product3.png|bezramki]] |
| − | pomiarów, do równań <xr id="eq:suma_syg">(%i)</xr> i <xr
| |
| − | id="eq:zal_lin">(%i)</xr> należy dodać element stochastyczny — nie
| |
| − | podlegający opisowi w ramach modelu szum <math>\epsilon</math>
| |
| − | ([[Reprezentacje przybliżone|patrz rozdział o reprezentacjach przybliżonych]]):
| |
| | | | |
| − | <equation id="eq:suma_z_szumem">
| + | [[Plik:Product4.png|bezramki]] |
| − | <math>\begin{matrix}
| |
| − | s(t) = \sum_{k=0}^{M} \alpha_k g_k + \epsilon_M \\
| |
| − | s(t) = \sum_{k=0}^{M} \alpha_k s (t - k \Delta t) + \epsilon_t
| |
| − | \end{matrix}</math>
| |
| − | </equation>
| |
| | | | |
| − | Na koniec zauważmy, że zaproponowane dotychczas modele mają postać
| + | [[Plik:Product5.png|bezramki]] |
| − | liniowych sum. Uwzględnienie nieliniowości otwiera nowe, nie
| |
| − | uwzględnione w tej książce rozdziały, jak np. chaos deterministyczny,
| |
| − | fraktale...
| |
| | | | |
| − | ==Sygnały ciągłe i dyskretne==
| + | [[Plik:Product6.png|bezramki]] |
| | | | |
| − | Wartości akcji w chwilach zamknięcia kolejnych sesji giełdy tworzą
| + | ===Liczby zespolone=== |
| − | sygnał z natury dyskretny. Jednak w przyrodzie większość stanowią
| |
| − | sygnały ciągłe, jak dźwięk (zmiany ciśnienia powietrza w czasie) czy
| |
| − | elektroencefalogram ([[EEG|EEG, potencjał elektryczny mózgu mierzony z
| |
| − | powierzchni czaszki]]). Niezależnie od tego, współczesna analiza
| |
| − | sygnałów odnosi się w praktyce głównie do sygnałów
| |
| − | dyskretnych. "Winne" są oczywiście komputery, urządzenia z natury
| |
| − | cyfrowe, czyli "rozumiejące" wyłącznie dyskretne wartości. Zastanówmy
| |
| − | się nad wynikającymi stąd korzyściami i stratami.
| |
| | | | |
| − | Jeśli sygnał z natury ciągły (np. dźwięk) zdecydujemy się analizować
| + | ===[[Szereg Fouriera]]=== |
| − | lub przechowywać w formie cyfrowej, to ciągłą funkcję (np. ciśnienia
| |
| − | powietrza) w czasie musimy zastąpić jej wartościami zmierzonymi w
| |
| − | określonych (najlepiej jednakowych) odstępach czasu, jak na
| |
| − | rys. <xr id="fig:7"> %i</xr>.
| |
| | | | |
| − | [[Plik:wstep_rys_2.jpg|thumb|center|600px|alt=próbkowanie zmienia ciągłys sygnał| <figure id="fig:7"></figure> Próbkowanie zamienia ciągły sygnał
| |
| − | (a) na punkty (b) o współrzędnych w chwilach
| |
| − | próbkowania i odpowiadających im wartościach sygnału ciągłego. Jeśli dysponujemy tylko
| |
| − | sygnałem próbkowanym (b), to możemy "uzupełnić" wartości spomiędzy próbek
| |
| − | przyjmując, że sygnał pomiędzy nimi jest np. liniowy (c) lub
| |
| − | stały od poprzedniego punktu (d) — widzimy rozbieżności z sygnałem oryginalnym (a).
| |
| − | Faktyczną reprezentacją funkcji po próbkowaniu jest ciąg liczb (e) plus znajomość odstępu próbkowania <math>\Delta t</math>. Optymalny sposób odzyskania wartości spomiędzy
| |
| − | próbek, jeśli próbkowanie przeprowadzono zgodnie z regułami sztuki, podaje [[STAT:Klasyczna#Twierdzenie_o_pr.C3.B3bkowaniu| rozdział o próbkowaniu]]]]
| |
| | | | |
| − | Przy przejściu z reprezentacji ciągłej (rys. <xr id="fig:7"> %i</xr> a) do dyskretnej (b) tracimy informację o
| |
| − | wartościach sygnału pomiędzy próbkami, a naiwne próby ich rekonstrukcji (c i d)
| |
| − | znacznie odbiegają od oryginału (a).
| |
| | | | |
| | + | ===[[Przekształcenie Fouriera]]=== |
| | | | |
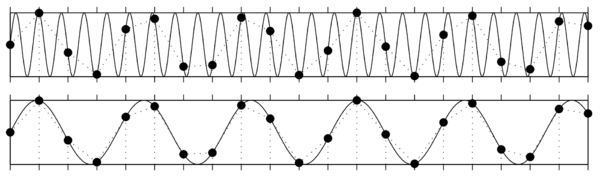
| − | [[Plik:wstep_rys_3.jpg|thumb|center|600px|alt=próbkowanie zmienia ciągłys sygnał| <figure id="fig:8"></figure> Próbkowane z częstością 1 oscylacje o częstościach ''f'', od góry: 1,3, 1, 0,5 i 0,3.
| |
| − | Sinusa o częstości 0,3 można odtworzyć dokładnie z samych wartości dyskretnych (kropki),
| |
| − | podobnie dla granicznej częstości 0,5. Natomiast próbkowane z tą samą częstością szybsze
| |
| − | oscylacje wprowadzają przekłamania — widoczna na samej górze oscylacja o częstości 1,3
| |
| − | daje w chwilach próbkowania wartości ''dokładnie takie same'' jak sygnał na dole.
| |
| − | Zjawisko to nosi nazwę ''aliasingu'' ([[STAT:Klasyczna#Przekszta.C5.82cenie_Fouriera_sygna.C5.82.C3.B3w_dyskretnych.2C_aliasing | porównaj)]].]]
| |
| | | | |
| | | | |
| − | Pomimo tego, cyfrowy zapis dźwięku (płyty CD)
| |
| − | zastąpił całkowicie
| |
| − | analogowe "czarne płyty" z winylu — dlaczego?
| |
| − | <ref>
| |
| − | Odpowiedź nie kryje się (niestety) w niższej cenie nośnika. Pomimo, że
| |
| − | technologia cyfrowa faktycznie pozwala na znacznie tańszą produkcję (tj.
| |
| − | powielanie) przy zachowaniu wysokiej jakości — jak wyjaśnimy za chwilę — to
| |
| − | jednak cena średnio dwukrotnie wyższa niż cena odp. płyty winylowej, która w
| |
| − | pierwszym okresie była uzasadniona wysokimi kosztami wprowadzania nowej
| |
| − | technologii, po jej rozpowszechnieniu pozostała na wywindowanym poziomie,
| |
| − | podwajając zyski wytwórni fonograficznych</ref>
| |
| − | * Po pierwsze, przy pewnych dodatkowych założeniach o sygnale ciągłym <math>s(t)</math>, możliwe jest jego ''dokładne'' odtworzenie z dyskretnej sekwencji próbek, jeśli odstęp próbkowania <math>\Delta t</math> dobrano odpowiednio dla danego sygnału. Mówi o tym twierdzenie Nyquista.
| |
| − | * Po drugie, zapis cyfrowy umożliwia korekcję błędów.
| |
| | | | |
| − | | + | <div align="right"> |
| − | | + | [[Analiza_sygnałów_-_wykład|⬆]] [[...|⮕]] |
| − | ===Zapis cyfrowy i korekcja błędów===
| + | </div> |
| − | Aby zrozumieć, dlaczego łatwość korekcji błędów związana jest z
| + | __NOTOC__ |
| − | zapisem cyfrowym, przyjrzyjmy się bliżej analogowym i cyfrowym zapisom
| |
| − | dźwięku. Na płycie analogowej dźwięk kodowany jest w zmiennym
| |
| − | wyżłobieniu rowka, w którym przemieszcza się igła gramofonu. W
| |
| − | przybliżeniu możemy wyobrazić sobie, że "podskok" igły w większym
| |
| − | wgłębieniu rowka odwzorowywany jest jako większe wychylenie membrany
| |
| − | głośnika (po zamianie w impuls elektryczny i przejściu przez
| |
| − | wzmacniacz). Tak więc wyżłobienie rowka płyty oryginalnie odwzorowuje
| |
| − | dokładnie zapisany dźwięk. Jego zarysowanie lub zabrudzenie wprowadzi
| |
| − | przy odtwarzaniu zakłócenia (zwykle trzaski). Jednoznaczne
| |
| − | rozróżnienie, które z wyżłobień rowka winylowej płyty odzwierciedlają
| |
| − | oryginalny zapis muzyki, a które powstały skutkiem uszkodzeń, jest
| |
| − | właściwie niemożliwe, dlatego też muzyka ze starych płyt kojarzy nam
| |
| − | się z obecnością trzasków i szumu.<ref>Tak naprawdę sprawa nie
| |
| − | jest beznadziejna:
| |
| − | * część zakłócen pochodzi z zanieczyszczeń; w tym przypadku zwykle pomaga delikatne czyszczenie płyty.
| |
| − | * Do pozostałych zakłóceń, których nie da się usunąć mechanicznie, stosuje się potężną metodologię analizy sygnałów (będącą przedmiotem następnych rozdziałów), która pomaga zgadnąć, które dźwięki w zapisie mogą pochodzić z zakłóceń. Zwykle jednak nie da się usunąć dokładnie wszystkich zakłóceń bez naruszenia brzmienia oryginału.</ref>
| |
| − | | |
| − | W przypadku zapisu cyfrowego możemy w prosty sposób ''wykryć'' fakt wystąpienie zakłóceń. Wyobraźmy sobie, że zapisujemy muzykę jako szereg liczb, opisujących amplitudę fali dźwiękowej mierzoną w ustalonych odstępach czasu (rys. <xr id="fig:9"></xr>; dla płyty kompaktowej <math>\Delta t = 1/44 100</math> sekundy). Ponieważ urządzenie, które będzie zamieniać ten zapis z powrotem na muzykę, i tak musi być swego rodzaju specjalizowanym komputerem (odtwarzaczem
| |
| − | CD), to do programu odtwarzającego możemy wprowadzić pewną modyfikację. Umówmy się dla przykładu, że z każdych dziesięciu kolejnych liczb, do zapisu muzyki będziemy wykorzystywać tylko
| |
| − | dziewięć, a ostatnią będziemy dobierać tak, żeby suma kolejnych dziesięciu liczb zawsze wynosiła np. milion.
| |
| − | | |
| − | [[Plik:wstep_rys_4.jpg|thumb|center|600px|alt=digitalizacja sygnału analogowego|<figure id="fig:9"></figure> Od góry: ciągły (analogowy) zapis fali dźwiękowej, poniżej próbkowanie, czyli wybór chwil, w których ją mierzymy, dalej zamiana zmierzonych wartości na liczby i liczb na bity. Pasek na dole może być np. fragmentem ścieżki na płycie CD: białe pola (zera) odbijają światło lasera, a czarne (jedynki) nie.]] | |
| − | | |
| − | Taki sposób zapisu wprowadza redundancję, czyli
| |
| − | nadmiar informacji w zapisie, ponieważ przy prawidłowym odczycie
| |
| − | wystarczyłoby znać dziewięć kolejnych liczb, aby wyznaczyć dziesiątą
| |
| − | (jako milion minus suma pozostałych dziewięciu). Jednak jeśli
| |
| − | wczytamy z takiego zapisu wszystkie liczby, i suma którejś dziesiątki
| |
| − | okaże się inna niz milion, to mamy pewność, że w tym miejscu wystąpił
| |
| − | błąd.<ref>Ale poprawna suma nie daje gwarancji, że błędu nie ma.
| |
| − | W jednej dziesiątce mogą wystąpić np. dwa jednakowe błędy o
| |
| − | przeciwnych znakach i suma pozostanie niezmieniona. Dlatego sumy
| |
| − | kontrolne liczy się w bardziej wyrafinowany sposób (np. CRC --
| |
| − | ''Cyclic Redundancy Check'' ) </ref> Taka informacja jest bardzo cenna:
| |
| − | * Jeśli ''jesteśmy pewni'' , że nagły skok amplitudy w kilku kolejnych próbkach jest wynikiem błędu zapisu, a nie efektem zamierzonym przez muzyka, to możemy ten skok "przemilczeć", czyli np. zastąpić "popsute" próbki średnią wartością poprzednich.
| |
| − | * Możemy zwiększyć redundancję i zapisać dwie jednakowe kopie; jeśli uszkodzeniu ulegnie fragment pierwszej kopii, program może automatycznie sięgnąć do odpowiedniego fragmentu drugiej kopii<ref>Prawdopodobieństwo wystąpienia uszkodzeń w tych samych fragmentach dwóch zapisów jest już bez porównania mniejsze niż pojedynczego uszkodzenia. Sposobem wprowadzania nadmiarowości, który minimalizuje prawdopodobieństwo wystąpienia takich pechowych przypadków, rządzi dość złożona matematyka z pogranicza statystyki, której nie będziemy tu omawiać. W każdym razie, dwie jednakowe kopie umieszczone jedna za drugą zwykle nie okazują się rozwiązaniem otymalnym.</ref>.
| |
| − | * W przypadku transmisji przez modem, program może zażądać powtórnego przesłania uszkodzonego fragmentu.
| |
| − | | |
| − | Niezależnie od tych korzyści, jeśli chcemy analizować sygnały z pomocą
| |
| − | komputera ''(maszyny cyfrowej)'', i tak jesteśmy "skazani" na
| |
| − | pracę z ich dyskretną formą.
| |
| − | | |
| − | Mimo tego, większość ogólnych twierdzeń będziemy rozważać w
| |
| − | przestrzeni funkcji ciągłych — o ile nie tyczą się ''explicite''
| |
| − | efektów próbkowania. Teoria funkcji ciągłych jest asymptotycznie
| |
| − | zgodna z wynikami dla sekwencji dyskretnych — dla odstępu próbkowania
| |
| − | dążącego do zera. Jej rezultaty, prostsze pojęciowo i łatwiejsze do
| |
| − | wyprowadzenia, są wystarczająco dokładne by wyjaśnić ogólne własności
| |
| − | dyskretnych obliczeń.
| |
| − | | |
| − | W uzasadnionych przypadkach będziemy oczywiście dyskutować efekty
| |
| − | próbkowania; w takich sytuacjach będziemy rozróżniać sygnał ciągły
| |
| − | <math>s(t)</math> od dyskretnej sekwencji <math>s[n]</math>.
| |
| − | | |
| − | [[TI:Technologia_Informacyjna/Cyfrowy_świat| Podobne tematy opisuje rozdział "Cyfrowy Świat"]] z podręcznika Technologii Informacyjnej.
| |