Szereg Fouriera

AS/ Szereg Fouriera

Sygnał okresowy (o okresie [math]T[/math]) można przedstawić w postaci szeregu Fouriera:

[math] \displaystyle s(t) =\sum_{n=-\infty}^{+\infty} c_n e^{-i\frac{2\pi n}{T} t}, [/math]

gdzie

[math] \displaystyle c_{n} = \frac{1}{T}\int_{0}^{T} s(t) e^{i \frac{2\pi n}{T} t} d t [/math]

Dowód: mnożymy obie strony pierwszego równania przez [math]e^\frac{2\pi i k t}{T}[/math] i całkujemy po [math]dt[/math] od [math]0[/math] do [math]T[/math]:

[math] \displaystyle \int_0^T s(t) e^{{{2\pi i k t}\over{T}}} dt = \sum_{n=-\infty}^{+\infty} \int_0^T c_n e^{i{{2 \pi (k-n)}\over{T}} t}dt [/math]

Całki po prawej stronie znikają dla [math]k \ne n[/math].

znikanie całki [math]\int_0^T e^{i{{2 \pi (k-n)}\over{T}} t}dt [/math] oznaczmy [math]m = k-n, m \in \mathbb N[/math]

[math]\displaystyle \int_0^T e^{i{{2 \pi m t}\over{T}} t}dt = \frac{i T}{2 \pi m} e^{i \frac{2 \pi m t}{T} }\bigg|_0^T = \frac{i T}{2 \pi m} \big( e^{i 2 \pi m} - 1 \big) = \frac{i T}{2 \pi m} \big( \cos(2 m \pi) - i \sin(2 m \pi) \big) [/math]

Jedyny niezerowy wyraz dla [math]k = n[/math] wynosi [math]\int_0^T c_n dt[/math], czyli [math]c_n T[/math] (bo [math]e^0=1[/math]). [math] \displaystyle \int_0^T s(t) e^{{{2\pi i k t}\over{T}}} dt = c_n T [/math]

Oznacza to, że każdą funkcję okresową możemy przedstawić w postaci sumy sinusów i kosinusów z odpowiednimi wagami — przypomnijmy [math]e^{i \phi} = \cos(\phi) + i \sin(\phi)[/math]. Wagi [math]c_n[/math] możemy traktować jako względny udział odpowiadających im częstości.

Tożsamość Parsevala dla szeregów Fouriera

[math] \frac{1}{T} \int_0^T \left| s(t) \right|^2 d t = \sum_{n=-\infty}^{\infty} \left| c_n \right|^2 [/math]

Dowód:

[math] \frac{1}{T} \int_0^T \left| s(t) \right|^2 d t =[/math]

[math] \frac{1}{T} \int_0^T s(t) \overline{s(t)} \,d t \; = [/math]

[math]\frac{1}{T} \int_0^T \left( \sum_{n=-\infty}^{+\infty} c_n e^{-i\frac{2\pi t}{T} n} \right) \left( \sum_{m=-\infty}^{+\infty} \overline{c_m} e^{i\frac{2\pi t}{T} m} \right) d t =[/math]

[math] \left\| \; \int_0^T e^{-i\frac{2\pi t}{T} n} e^{i\frac{2\pi t}{T} m}= \delta_{(m-n)} T \;\right\|\; =[/math]

[math]\sum_{n = -\infty}^{\infty} c_n \overline{c_n} \;\;= \sum_{n = -\infty}^{\infty} |c_n|^2 [/math]

Energia, moc, widmo

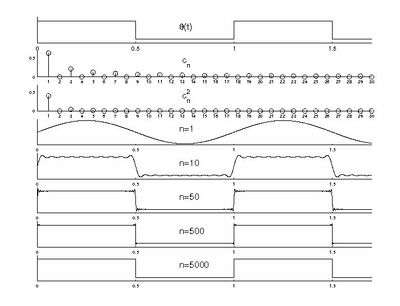
Jeśli sygnałem będzie np. prąd elektryczny, płynący w obwodzie o jednostkowej oporności w czasie od [math]0[/math] do [math]T[/math], to wytracona przez niego energia wyniesie [math]\int_0^T s(t)^2 d t[/math]. W ogólności, biorąc pod uwagę sygnały o wartościach zespolonych, całkowitą energię sygnału definiujemy jako [math]\int_{-\infty}^{\infty} | s(t) |^2 d t[/math]. Moc to oczywiście energia wytracana w jednostce czasu, czyli [math]\frac{1}{T}\int_{0}^{T} | s(t) |^2 d t[/math]. Jak widać z powyższego twierdzenia, dla sygnałów okresowych możemy ją również obliczać jako sumę kwadratów współczynników szeregu Fouriera [math]\sum c_n^2[/math]. Pozwala to interpretować [math]c_n^2[/math] jako moc, niesioną przez odpowiadającą mu częstość. Wykres tej wielkości w zależności od częstości nazywamy widmem mocy sygnału. Dla sygnału okresowego widmo mocy będzie dyskretne (patrz rysunek 1).

Wszystko to nie tyczy się li tylko sygnałów czysto okresowych; z sygnału nie-okresowego [math]s(t)[/math], określonego na skończonym przedziale [math][0, T][/math], możemy utworzyć sygnał okresowy [math]s_T(t)[/math]:

[math]\begin{matrix} s_T(t)=s(t),\;t\in[0,T] \\ s_T(t+nT)=s(t),\;n=1,2,\ldots \end{matrix}[/math]

tożsamy z [math]s(t)[/math] w przedziale [math][0, T][/math], który można już przedstawić w postaci sumy 1.

Rozwinięcie prostokąta w szereg Fouriera Policzmy postać współczynników Fouriera dla funkcji [math]\Theta(t)[/math] (Figure 1), określonej na przedziale [math][0,1][/math] w następujący sposób:

[math] \Theta(t) = \left\{ \begin{matrix} 1 &, & t \in [0, \frac{1}{2})\\ 0 &, & t \in [ \frac{1}{2}, 1] \end{matrix} \right. [/math]

Bezpośrednio z wzoru 2 dostajemy (dla [math]T = 1[/math])

[math]\begin{matrix} c_{n} = \frac{1}{T}\int_{0}^{T} \Theta(t) e^\frac{i 2\pi n t}{T} d t = \int_{0}^\frac{1}{2} e^{{{i 2\pi n t}}} d t = ( \mathrm{dla}\; n \ne 0 ) = \left [\frac{1}{i 2\pi n} e^{{i 2\pi n t}} \right ]_{t=0}^{t=\frac{1}{2}} \\ = \frac{1}{i 2\pi n} ( e^{i \pi n} - 1 ) = \left\{ \begin{matrix} 0 & \mathrm{dla}\; n = \pm2, \pm4, \ldots\\ i/\pi n & \mathrm{dla}\; n = \pm1, \pm3, \ldots \end{matrix} \right .\\ (\mathrm{dla}\; n=0) \;\; c_0 = \int_{0}^\frac{1}{2} 1 d t = \frac{1}{2} \end{matrix}[/math]

Tak więc z wzoru 1

[math]\begin{matrix} \Theta(t) = \sum_{-\infty}^{\infty} c_n e^{-i 2 \pi t n} = \frac{1}{2}\; + \sum_{n=\pm1, \pm3, \ldots} \frac{i}{\pi n} e^{-i 2 \pi t n}= \\ = \frac{1}{2}\; + \sum_{n=\pm1, \pm3, \ldots} \frac{i}{\pi n} \left( \cos(2\pi n t) - i \sin( 2\pi n t) \right)=\\ = \frac{1}{2}\; + \sum_{n=\pm1, \pm3, \ldots} \frac{i}{\pi n} \cos(2\pi n t)\;\; + \sum_{n=\pm1, \pm3, \ldots} \frac{1}{\pi n} \sin( 2\pi n t) \end{matrix}[/math]

W sumie kosinusów wyrazy dla [math]n\gt 0[/math] znoszą odpowiednie wyrazy dla [math]-n[/math] (bo [math]cos(-x)=cos(x)[/math]), w sumie sinusów wyrazy dla [math]\pm n[/math] dodają się (bo [math]sin(-x)=-sin(x)[/math]), dając w efekcie

[math] \Theta(t) = \frac{1}{2} + \frac{2}{\pi}\sum_{n=1}^{\infty} \frac{\sin\left(2\pi (2n-1) t\right)}{(2n-1)} [/math]

Od góry, kolejno: funkcja [math]\Theta[/math] (równanie %i 4), "uzupełniona" do funkcji okresowej według wzoru %i 3, pierwszych 30 współczynników szeregu Fouriera, kwadraty współczynników szeregu Fouriera — dyskretne widmo, pierwszy wyraz rozwinięcia Fouriera, sumy pierwszych 10, 50, 500 i 5000 wyrazów rozwinięcia (5). Jak widać, najtrudniejsza do wyrażenia z pomocą funkcji trygonometrycznych jest nieciągłość funkcji [math]\theta(t)[/math] w punktach [math]\left\{\pm \frac{k}{2}, k \in N \right\}[/math]; niejednorodna zbieżność szeregów Fouriera w tych rejonach nosi nazwę efektu Gibbsa.

⬆ ⮕