Wstep: Różnice pomiędzy wersjami
| (Nie pokazano 95 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
| − | ==[[Analiza_sygnałów_- | + | ==[[Analiza_sygnałów_-_wykład|⬆]] Próbkowanie sygnałów analogowych== |
| − | + | Sygnały zapisujemy, przetwarzamy i analizujemy w postaci ciągów liczb. Przejście od sygnału ciągłego do cyfrowego odbywa się przez proces próbkowania, czyli zapisywania kolejnych amplitud sygnału w ustalonych, stałych odstępach czasu, [[TI/Cyfrowy_świat|omawiany wcześniej na TIiK]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Plik:AD.png|220px|bezramki]] | |
| − | + | <!--Ciągły sygnał z górnego rysunku, po próbkowaniu w punktach symbolizowanych czarnymi kropkami na rysunku dolnym, na dysku zostaje zapisany jako ciąg liczb:--> | |
| − | + | 102, 195, 80, 16, 147, 178 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Żeby odtworzyć fizyczne własności sygnału, czyli narysować zapisane wartości próbek w odpowiedniej skali, musimy znać ''częstość próbkowania'' i ''stałą kalibracji''. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Wyrażana w hercach (Hz) częstość próbkowania (ang. ''sampling frequency'', <math>f_s</math>) to liczba próbek na sekundę. Jest ona odwrotnością odstępu w czasie między kolejnymi próbkami (<math>\Delta t</math>): | |
| − | + | <div align = "center> | |
| − | + | <math>f_s = \dfrac{1}{\Delta t}</math> | |
| − | + | </div> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Stała kalibracji to współczynnik, przez który mnożymy zapisane liczby, żeby otrzymać wartości w jednostkach fizycznych, na przykład mikrowoltach. | |
| − | |||
| − | |||
| − | + | Oczywiście musimy też wiedzieć, w jakim formacie zapisano na dysku liczby (formaty omawialiśmy na wykładzie o [[TI/Zera_i_jedynki|binarnych reprezentacjach liczb]]), oraz, w przypadku sygnałów wielozmiennych o jednolitym próbkowaniu, znać liczbę kanałów. Taka dodatkowa informacja (metainformacja) jest konieczna do poprawnego wyświetlenia danych z pliku, w którym zapisano dane wielokanałowe, jak np. kilka odprowadzeń EEG lub dane kilku spółek giełdowych, próbkowane i zapisywane w jednakowych odstępach czasu. | |
| − | |||
| − | |||
| − | (.. | ||
| − | + | [[Plik:WakeEEG Svarog 3chans.png|1200px|bezramki]] | |
| − | + | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | |
| + | | <strong>Informacje o częstości próbkowania, stałej kalibracji, liczbie i nazwach kanałów itp. to metainformacja, klucz do poprawnego odczytu i intepretacji zapisanych liczb.</strong> | ||
| + | |- | ||
| + | |Zawartość pliku "wakeEEG.xml", zawierającego metainformację określającą sposób wyświetlania i opisu liczb zawartych w pliku "wakeEEG.bin" według formatu opracowanego na WF UW w programie Svarog: | ||
| + | <pre> | ||
| + | <?xml version="1.0" encoding="UTF-8" standalone="no"?> | ||
| + | <rs:rawSignal xmlns:rs="http://signalml.org/rawsignal"> | ||
| + | <rs:exportFileName>moto128.bin</rs:exportFileName> | ||
| + | <rs:sourceFileName>durka_moto3.bin</rs:sourceFileName> | ||
| + | <rs:sourceFileFormat> | ||
| + | <rs:rawSignalInfo/> | ||
| + | </rs:sourceFileFormat> | ||
| + | <rs:samplingFrequency>128.0</rs:samplingFrequency> | ||
| + | <rs:channelCount>20</rs:channelCount> | ||
| + | <rs:sampleCount>20480</rs:sampleCount> | ||
| + | <rs:sampleType>FLOAT</rs:sampleType> | ||
| + | <rs:byteOrder>LITTLE_ENDIAN</rs:byteOrder> | ||
| + | <rs:pageSize>20.0</rs:pageSize> | ||
| + | <rs:blocksPerPage>1</rs:blocksPerPage> | ||
| + | <rs:eegSystemName> | ||
| + | <rs:eegSystemSymbol>EEG 10_20 Cap19</rs:eegSystemSymbol> | ||
| + | <rs:eegSystemType>adults</rs:eegSystemType> | ||
| + | </rs:eegSystemName> | ||
| + | <rs:channelLabels> | ||
| + | <rs:label>Fp1</rs:label> | ||
| + | <rs:label>Fp2</rs:label> | ||
| + | <rs:label>F7</rs:label> | ||
| + | <rs:label>F3</rs:label> | ||
| + | <rs:label>Fz</rs:label> | ||
| + | <rs:label>F4</rs:label> | ||
| + | <rs:label>F8</rs:label> | ||
| + | <rs:label>T7</rs:label> | ||
| + | <rs:label>C3</rs:label> | ||
| + | <rs:label>Cz</rs:label> | ||
| + | <rs:label>C4</rs:label> | ||
| + | <rs:label>T8</rs:label> | ||
| + | <rs:label>P7</rs:label> | ||
| + | <rs:label>P3</rs:label> | ||
| + | <rs:label>Pz</rs:label> | ||
| + | <rs:label>P4</rs:label> | ||
| + | <rs:label>P8</rs:label> | ||
| + | <rs:label>O1</rs:label> | ||
| + | <rs:label>O2</rs:label> | ||
| + | <rs:label>FCz</rs:label> | ||
| + | </rs:channelLabels> | ||
| + | <rs:exportDate>2013-03-20T12:59:21</rs:exportDate> | ||
| + | <rs:calibrationGain> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.01</rs:calibrationParam> | ||
| + | </rs:calibrationGain> | ||
| + | <rs:calibrationOffset> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | <rs:calibrationParam>0.1</rs:calibrationParam> | ||
| + | </rs:calibrationOffset> | ||
| + | </rs:rawSignal> | ||
| + | </pre> | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | + | ==Aliasing i częstość Nyquista== |
| − | <math> | + | [[Plik:Aliasing gif.gif|590px|bezramki]] |
| − | + | ||
| − | </math> | + | W procesie próbkowania kluczową rolę odgrywa twierdzenie o próbkowaniu (inaczej twierdzenie Nyquista-Shannona, czasem w skrócie twierdzenie Nyquista). Mówi ono, że sygnał ciągły możemy odtworzyć za zapisanych próbek, jeśli częstość próbkowania <math>f_s</math> była wyższa niż dwukrotność najwyższej z występujących w sygnale częstości <math>f_{max}</math>, nazywana częstością Nyquista <math>f_N</math>: |
| − | </ | + | <div align = "center> |
| + | <math> f_s = \dfrac{1}{\Delta t} > 2* f_{max} = f_N</math> | ||
| + | </div> | ||
| + | Jeśli częstość próbkowania nie była wystarczająco wysoka, nie tylko stracimy informację o zmianach amplitudy sygnału "pomiędzy próbkami", ale dojdzie też do zafałszowania sygnału w niższych częstościach, które z pozoru nie powinny być zaburzone. Efekt ten jest bliżej omówiony w rozdziale [[Aliasing]]. | ||
| + | |||
| + | [[Plik:Nyquist1.png|600px|bezramki]] | ||
| + | |||
| + | ==Sygnał dyskretny jako wektor== | ||
| + | [[Plik:AD.png|mały|220px|<pre>102, 195, 80, 16, 147, 178</pre>]] | ||
| + | Skoro sygnał to po prostu ciąg liczb, możemy go potraktować jak wektor. Na płaszczyźnie wektor to para współrzędnych (''x'', ''y''), w przestrzeni trójwymiarowej trójka liczby (x, y, z), które wyobrażamy sobie jako strzałkę wiodącą od punktu (0, 0, 0) do (x, y, z). Sygnał składający się z pięciu punktów będzie wektorem w przestrzeni pięciowymiarowej, więc intuicja "strzałki" dla większości z nas przestaje być użyteczna. Pomimo tego, możemy wciąż korzystać z użytecznych pojęć z dziedziny algebry wektorów, jak ortogonalność czy iloczyn skalarny. | ||
| + | |||
| + | |||
| + | ===Iloczyn skalarny=== | ||
| + | Iloczyn skalarny przyjmiemy jako miarę podobieństwa dwóch sygnałów. Obliczać go będziemy tak samo jak dla wektorów — przypomnijmy: niech <math>\mathbf{x} = [x_1, x_2, x_3]</math>, i <math>\mathbf{y} = [y_1, y_2, y_3]</math>; iloczyn skalarny tych wektorów oznaczamy <math display="block">\mathbf x \cdot \mathbf y</math> (''zarówno wytłuszczenie symboli wektorów, jak i symbol mnożenia/ilocznu skalarnego "<math>\cdot</math>", będziemy dalej pomijać''): | ||
| + | |||
| + | <div align = "center"> | ||
| + | <math display="block">\displaystyle \mathbf a \cdot \mathbf b = \sum_{i=1}^3 x_i y_i = x_1 y_1 + x_2 y_2 + x_3 y_3</math> | ||
| + | </div> | ||
| + | |||
| + | A jak to będzie wyglądać dla sygnałów złożonych z więcej niż trzech punktów? Weźmy | ||
| + | |||
| + | <math>x=[-2, -2, 2, -1, -2]</math> | ||
| + | |||
| + | <math>y=[-1, -1, 1, 1, 0]</math> | ||
| + | |||
| + | Zamiast strzałek w pięciowymiarowej przestrzeni, łatwiej wizualizować na wykresach wartości kolejnych próbek: | ||
| + | |||
| + | [[Plik:Product2.png|bezramki]] | ||
| + | |||
| + | <math>x\cdot y = [-2, -2, 2, -1, -2] \cdot [-1, -1, 1, 1, 0] = 2+2+2-1+0 = 5</math> | ||
| + | |||
| + | |||
| + | |||
| + | ===Ortogonalność=== | ||
| + | Kolejnym użytecznym pojęciem, które możemy zaczerpnąć bezpośrednio z algebry wektorów, jest ortogonalność. Dwa wektory (sygnały) są do siebie ortogonalne, jeśli ich iloczyn skalarny wynosi zero, jak poniżej: | ||
| + | |||
| + | [[Plik:Product6.png|500px|bezramki]] | ||
| + | |||
| + | W przypadku sygnału złożonego z 16 punktów, możemy ten fakt sprawdzić obliczając iloczyn skalarny punkt po punkcie, albo też zauważając prawidłowości występujące w każdym okresie górnego sygnału. W przypadku dłuższych i bardziej złożonych sygnałów może to już nie być takie oczywiste, jak np. ortogonalność wszystkich sinusów na poniższym rysunku, których częstości są całkowitymi wielokrotnościami częstości podstawowej: | ||
| + | |||
| + | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| + | | <strong>Zbiór ortogonalnych sinusów</strong> | ||
| + | |- | ||
| + | |<math>f(x)=\sin(kx), k=1,2,\ldots</math> | ||
| + | [[Plik:Ort sines cont.png|700px|bezramki]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | ===Energia sygnału=== | ||
| + | Matematycznie energia sygnału <math>x</math> to <math>\langle x,x \rangle</math> (czyli <math>x\cdot x</math>, iloczyn skalarny sygnału "z samym sobą"). Dla sygnałów ciągłych <math>\langle x(t), x(t) \rangle = \int |x(t)|^2 dt</math>, dla sygnałów dyskretnych <math> \langle x[n], x[n] \rangle = \sum_n |x[n]|^2</math>. | ||
| + | Fizycznie musimy wziąć pod uwagę wspomniane wcześniej stałą kalibracji i częstość próbkowania: | ||
| + | |||
| + | *Jeśli sygnałem będzie prąd elektryczny o natężeniu <math>i(t)</math> mierzonym w amperach, płynący w obwodzie o oporności <math>R</math> omów, to wytracana przez niego energia wyniesie <math>E_i = R \int |i(t)|^2 dt</math> dżuli. | ||
| + | |||
| + | *W przypadku sygnału dyskretnego <math>x[t]</math>, całkę <math>\int x(t) dt </math> zastępujemy sumą pól kolejnych prostokątów o wysokości <math>x[n]</math> i szerokości równej odstępowi między kolejnymi punktami <math>\Delta t = \frac{1}{f_s}</math> | ||
| + | :<math>E_{x[n]} = \Delta t \sum_n |x(n)|^2 = \frac{1}{f_s} \sum_n |x(n)|^2 </math> | ||
| + | |||
| + | |||
| + | [[Plik:Product3.png|bezramki]] | ||
| + | |||
| + | <!-- | ||
| + | <math>x\cdot x = [-2, -2, 2, -1, -2] \cdot [-2, -2, 2, -1, -2] = 4+4+4+1+4=17</math> | ||
| + | --> | ||
| + | |||
| + | ==Liczby zespolone== | ||
| + | Przypomnijmy w skrócie: <math>i^2=-1</math>. Liczbę zespoloną <math>z</math> możemy zapisać w postaci algebraicznej jako | ||
| + | : <math>z=a+bi,</math> | ||
| + | gdzie <math>a</math> to część rzeczywista, <math>b</math> — część urojona. | ||
| + | |||
| + | Sprzężenie zespolone liczby <math>z</math> oznaczamy <math>\overline{z}</math>: | ||
| + | : <math>\overline{z} = a - bi</math> | ||
| + | a jej moduł to <math>|z| = \sqrt{a^2 + b^2}</math> (inaczej <math>|z| = z \cdot \overline{z}</math>). | ||
| + | |||
| + | Postać trygonometryczna: | ||
| + | : <math>z = a + bi = |z| \cdot \dfrac{a}{|z|} + |z| \cdot \dfrac{b}{|z|}i = |z| \cdot (\cos \phi + i\sin \phi).</math> | ||
| + | |||
| + | Wykorzystując wzór Eulera<ref>wzorem Eulera bywa również nazywane równanie <math>e^{i\pi}+1=0</math></ref> | ||
| + | :<math>e^{i\phi} = \cos(\phi) + i\sin(\phi)</math> | ||
| + | możemy liczbę zespoloną zapisać jako | ||
| + | :<math>z = |z|e^{i\phi}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==[[Szereg Fouriera]]== | ||
| + | Sygnał ''okresowy'' (o okresie <math>T</math>) można przedstawić w | ||
| + | postaci szeregu Fouriera: | ||
| − | + | <equation id="eq:15"> | |
| − | + | <math> | |
| − | + | s(t) =\sum_{n=-\infty}^{+\infty} c_n e^{-i\frac{2\pi n}{T} t}, | |
| − | + | </math> | |
| + | </equation> | ||
| − | <equation id="eq: | + | gdzie |
| + | <equation id="eq:16"> | ||
<math> | <math> | ||
| − | + | c_{n} = \frac{1}{T}\int_{0}^{T} s(t) e^{i \frac{2\pi n}{T} t} d t | |
</math> | </math> | ||
| − | </equation> | + | </equation> |
| − | + | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | |
| − | + | | <strong>'''Dowód''' powyższego wzoru: </strong> | |
| − | id="eq: | + | |- |
| − | + | | Mnożymy obie strony <xr id="eq:15">równania</xr> przez <math>e^\frac{2\pi i k t}{T}</math> | |
| − | + | i całkujemy po <math>dt</math> od <math>0</math> do <math>T</math>: | |
| − | < | + | <math> |
| − | + | \int_0^T s(t) e^{{{2\pi i k t}\over{T}}} dt = | |
| − | s(t) = \sum_{ | + | \sum_{n=-\infty}^{+\infty} \int_0^T c_n e^{i{{2 \pi (k-n)}\over{T}} t}dt |
| − | + | </math> | |
| − | \ | + | |
| − | + | Całki po prawej stronie znikają dla <math>k \ne n</math>. Jedyny niezerowy | |
| + | wyraz dla <math>k = n</math> wynosi <math>\int_0^T c_n dt</math>, czyli <math>c_n T</math> (bo <math>e^0=1</math>). | ||
| + | |} | ||
| + | Każdą funkcję okresową możemy przedstawić w postaci sumy sinusów i kosinusów z odpowiednimi wagami — przypomnijmy: <math>e^{i \phi} = \cos(\phi) + i \sin(\phi)</math>. | ||
| − | + | Wagi <math>c_n</math> możemy traktować jako względny udział odpowiadających im częstości. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Przykład: szereg Fouriera dla prostokąta=== | |
| − | + | Policzmy postać współczynników Fouriera dla funkcji <math>\Theta(t)</math>, | |
| − | + | określonej na przedziale <math>[0,1]</math> w następujący sposób: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | :<equation id="eq:18"> | |
| − | + | <math> | |
| − | + | \Theta(t) = \left\{ | |
| − | + | \begin{matrix} | |
| − | + | 1 &, & t \in [0, \frac{1}{2})\\ | |
| + | 0 &, & t \in [ \frac{1}{2}, 1] | ||
| + | \end{matrix} | ||
| + | \right. | ||
| + | </math> | ||
| + | </equation> | ||
| + | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| + | | <strong>obliczenia: </strong> | ||
| + | |- | ||
| + | |Bezpośrednio z <xr id="eq:16">wzoru</xr> dostajemy (dla <math>T = 1</math>) | ||
| + | |||
| + | <math>\begin{matrix} | ||
| + | c_{n} = \frac{1}{T}\int_{0}^{T} \Theta(t) e^\frac{i 2\pi n t}{T} d t | ||
| + | = \int_{0}^\frac{1}{2} e^{{{i 2\pi n t}}} d t = ( \mathrm{dla}\; n \ne 0 ) = | ||
| + | \left [\frac{1}{i 2\pi n} e^{{i 2\pi n t}} \right ]_{t=0}^{t=\frac{1}{2}} \\ | ||
| + | = \frac{1}{i 2\pi n} ( e^{i \pi n} - 1 ) = | ||
| + | \left\{ | ||
| + | \begin{matrix} | ||
| + | 0 & \mathrm{dla}\; n = \pm2, \pm4, \ldots\\ | ||
| + | i/\pi n & \mathrm{dla}\; n = \pm1, \pm3, \ldots | ||
| + | \end{matrix} | ||
| + | \right .\\ | ||
| + | (\mathrm{dla}\; n=0) \;\; c_0 = \int_{0}^\frac{1}{2} 1 d t = \frac{1}{2} | ||
| + | \end{matrix}</math> | ||
| + | <br/> | ||
| + | <br/> | ||
| − | + | Tak więc z <xr id="eq:15">wzoru</xr> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <math>\begin{matrix} | |
| − | + | \Theta(t) = \sum_{-\infty}^{\infty} c_n e^{-i 2 \pi t n} = | |
| − | + | \frac{1}{2}\; + \sum_{n=\pm1, \pm3, \ldots} \frac{i}{\pi n} e^{-i 2 \pi t n}= \\ | |
| + | = \frac{1}{2}\; + \sum_{n=\pm1, \pm3, \ldots} \frac{i}{\pi n} \left( \cos(2\pi n t) - i \sin( 2\pi n t) \right)=\\ | ||
| + | = \frac{1}{2}\; + \sum_{n=\pm1, \pm3, \ldots} \frac{i}{\pi n} \cos(2\pi n t)\;\; + \sum_{n=\pm1, \pm3, \ldots} \frac{1}{\pi n} \sin( 2\pi n t) | ||
| + | \end{matrix}</math> | ||
| − | + | W sumie kosinusów wyrazy dla <math>n>0</math> znoszą odpowiednie wyrazy dla <math>-n</math> (bo <math>cos(-x)=cos(x)</math>), w sumie | |
| − | + | sinusów wyrazy dla <math>\pm n</math> dodają się (bo <math>sin(-x)=-sin(x)</math>) | |
| − | + | |} | |
| − | + | Dostajemy | |
| − | |||
| − | |||
| + | <equation id="eq:19"> | ||
| + | <math> | ||
| + | \displaystyle \Theta(t) = \frac{1}{2} + \frac{2}{\pi}\sum_{n=1}^{\infty} \frac{\sin\left(2\pi (2n-1) t\right)}{(2n-1)} | ||
| + | </math> | ||
| + | </equation> | ||
| − | + | [[Plik:klasyczna_rys_2.png|bezramki|centruj|600px]] | |
| − | + | <!--|<figure id="fig:20"></figure>Od góry, kolejno: | |
| − | + | funkcja <math>\Theta</math> (<xr id="eq:18">równanie </xr>) uzupełniona do funkcji okresowej, pierwszych 30 współczynników szeregu Fouriera, | |
| − | < | + | kwadraty współczynników szeregu Fouriera — dyskretne widmo, |
| − | + | pierwszy wyraz rozwinięcia Fouriera, sumy pierwszych 10, 50, 500 i 5000 wyrazów <xr id="eq:19">rozwinięcia</xr>. <br> | |
| − | + | Jak widać, najtrudniejsza do wyrażenia z pomocą funkcji | |
| − | + | trygonometrycznych jest nieciągłość funkcji <math>\theta(t)</math> w punktach <math>\left\{\pm \frac{k}{2}, k \in N \right\}</math>; niejednorodna | |
| − | + | zbieżność szeregów Fouriera w tych rejonach nosi nazwę ''efektu Gibbsa''.]] | |
| − | + | --> | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | Od góry, kolejno: | ||
| + | funkcja <math>\Theta</math> (<xr id="eq:18">równanie </xr>) uzupełniona do funkcji okresowej, pierwszych 30 współczynników szeregu Fouriera, | ||
| + | kwadraty współczynników szeregu Fouriera — dyskretne widmo, | ||
| + | pierwszy wyraz rozwinięcia Fouriera, sumy pierwszych 10, 50, 500 i 5000 wyrazów <xr id="eq:19">rozwinięcia</xr>. <br> | ||
| + | Jak widać, najtrudniejsza do wyrażenia z pomocą funkcji | ||
| + | trygonometrycznych jest nieciągłość funkcji <math>\theta(t)</math> w punktach <math>\left\{\pm \frac{k}{2}, k \in N \right\}</math>; niejednorodna | ||
| + | zbieżność szeregów Fouriera w tych rejonach nosi nazwę ''efektu Gibbsa''. | ||
| + | ==[[Przekształcenie Fouriera]]== | ||
| + | Przejdźmy do nieskończoności z okresem sygnału: <math>T\rightarrow\infty</math>. | ||
| + | Wtedy odstęp <math>\left(\frac{2\pi}{T}\right)</math> | ||
| + | między częstościami kolejnych elementów sumy szeregu Fouriera | ||
| − | + | <math>\displaystyle | |
| − | + | s(t) =\sum_{n=-\infty}^{+\infty} c_n e^{-i\frac{2\pi t}{T} n}, | |
| − | + | </math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | dąży do <math>0</math> i suma przechodzi w całkę | |
| − | |||
| − | |||
| − | + | <equation id="eq:21"> | |
| + | <math>\displaystyle | ||
| + | s(t)=\int_{-\infty}^{\infty}\hat{s}(f)e^{-i 2\pi t f} d f | ||
| + | </math> | ||
| + | </equation> | ||
| + | |||
| + | funkcja <math>\hat{s}(f)</math>, zastępująca dyskretny ciąg współczynników szeregu Fouriera | ||
| − | + | <math>\displaystyle | |
| − | + | c_{n} = \frac{1}{T}\int_{0}^{T} s(t) e^\frac{2\pi i n t}{T} d t | |
| − | + | </math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | to '''transformata Fouriera''' sygnału <math>s(t)</math>, czyli wynik działania przekształcenia (transformacji) Fouriera <math>\mathcal{F}</math>. | |
| − | |||
| − | |||
| − | + | <equation id="eq:22"> | |
| − | + | <math>\displaystyle | |
| − | + | \mathcal{F}\left( s(t) \right) \equiv \hat{s}(f)=\int_{-\infty}^{\infty}s(t)e^{i 2\pi f t} d t | |
| − | + | </math> | |
| − | + | </equation> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[ | + | <div align="right"> |
| + | [[Analiza_sygnałów_-_wykład|⬆]] [[Szereg_Fouriera|⮕]] | ||
| + | </div> | ||
Aktualna wersja na dzień 17:24, 16 lis 2024
Spis treści
⬆ Próbkowanie sygnałów analogowych
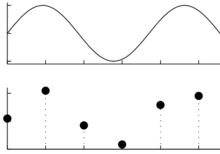
Sygnały zapisujemy, przetwarzamy i analizujemy w postaci ciągów liczb. Przejście od sygnału ciągłego do cyfrowego odbywa się przez proces próbkowania, czyli zapisywania kolejnych amplitud sygnału w ustalonych, stałych odstępach czasu, omawiany wcześniej na TIiK.
102, 195, 80, 16, 147, 178
Żeby odtworzyć fizyczne własności sygnału, czyli narysować zapisane wartości próbek w odpowiedniej skali, musimy znać częstość próbkowania i stałą kalibracji.
Wyrażana w hercach (Hz) częstość próbkowania (ang. sampling frequency, [math]f_s[/math]) to liczba próbek na sekundę. Jest ona odwrotnością odstępu w czasie między kolejnymi próbkami ([math]\Delta t[/math]):
[math]f_s = \dfrac{1}{\Delta t}[/math]
Stała kalibracji to współczynnik, przez który mnożymy zapisane liczby, żeby otrzymać wartości w jednostkach fizycznych, na przykład mikrowoltach.
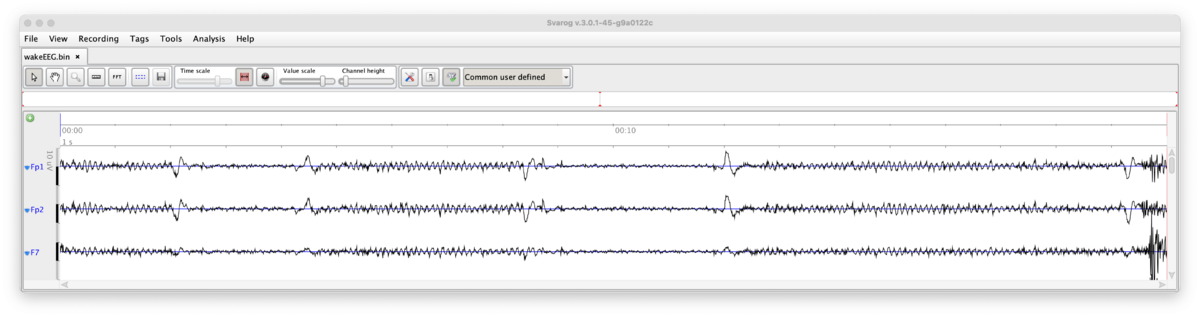
Oczywiście musimy też wiedzieć, w jakim formacie zapisano na dysku liczby (formaty omawialiśmy na wykładzie o binarnych reprezentacjach liczb), oraz, w przypadku sygnałów wielozmiennych o jednolitym próbkowaniu, znać liczbę kanałów. Taka dodatkowa informacja (metainformacja) jest konieczna do poprawnego wyświetlenia danych z pliku, w którym zapisano dane wielokanałowe, jak np. kilka odprowadzeń EEG lub dane kilku spółek giełdowych, próbkowane i zapisywane w jednakowych odstępach czasu.
| Informacje o częstości próbkowania, stałej kalibracji, liczbie i nazwach kanałów itp. to metainformacja, klucz do poprawnego odczytu i intepretacji zapisanych liczb. |
Zawartość pliku "wakeEEG.xml", zawierającego metainformację określającą sposób wyświetlania i opisu liczb zawartych w pliku "wakeEEG.bin" według formatu opracowanego na WF UW w programie Svarog:
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<rs:rawSignal xmlns:rs="http://signalml.org/rawsignal">
<rs:exportFileName>moto128.bin</rs:exportFileName>
<rs:sourceFileName>durka_moto3.bin</rs:sourceFileName>
<rs:sourceFileFormat>
<rs:rawSignalInfo/>
</rs:sourceFileFormat>
<rs:samplingFrequency>128.0</rs:samplingFrequency>
<rs:channelCount>20</rs:channelCount>
<rs:sampleCount>20480</rs:sampleCount>
<rs:sampleType>FLOAT</rs:sampleType>
<rs:byteOrder>LITTLE_ENDIAN</rs:byteOrder>
<rs:pageSize>20.0</rs:pageSize>
<rs:blocksPerPage>1</rs:blocksPerPage>
<rs:eegSystemName>
<rs:eegSystemSymbol>EEG 10_20 Cap19</rs:eegSystemSymbol>
<rs:eegSystemType>adults</rs:eegSystemType>
</rs:eegSystemName>
<rs:channelLabels>
<rs:label>Fp1</rs:label>
<rs:label>Fp2</rs:label>
<rs:label>F7</rs:label>
<rs:label>F3</rs:label>
<rs:label>Fz</rs:label>
<rs:label>F4</rs:label>
<rs:label>F8</rs:label>
<rs:label>T7</rs:label>
<rs:label>C3</rs:label>
<rs:label>Cz</rs:label>
<rs:label>C4</rs:label>
<rs:label>T8</rs:label>
<rs:label>P7</rs:label>
<rs:label>P3</rs:label>
<rs:label>Pz</rs:label>
<rs:label>P4</rs:label>
<rs:label>P8</rs:label>
<rs:label>O1</rs:label>
<rs:label>O2</rs:label>
<rs:label>FCz</rs:label>
</rs:channelLabels>
<rs:exportDate>2013-03-20T12:59:21</rs:exportDate>
<rs:calibrationGain>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
<rs:calibrationParam>0.01</rs:calibrationParam>
</rs:calibrationGain>
<rs:calibrationOffset>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
<rs:calibrationParam>0.1</rs:calibrationParam>
</rs:calibrationOffset>
</rs:rawSignal>
|
Aliasing i częstość Nyquista
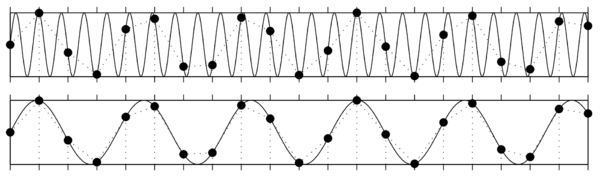
W procesie próbkowania kluczową rolę odgrywa twierdzenie o próbkowaniu (inaczej twierdzenie Nyquista-Shannona, czasem w skrócie twierdzenie Nyquista). Mówi ono, że sygnał ciągły możemy odtworzyć za zapisanych próbek, jeśli częstość próbkowania [math]f_s[/math] była wyższa niż dwukrotność najwyższej z występujących w sygnale częstości [math]f_{max}[/math], nazywana częstością Nyquista [math]f_N[/math]:
[math] f_s = \dfrac{1}{\Delta t} \gt 2* f_{max} = f_N[/math]
Jeśli częstość próbkowania nie była wystarczająco wysoka, nie tylko stracimy informację o zmianach amplitudy sygnału "pomiędzy próbkami", ale dojdzie też do zafałszowania sygnału w niższych częstościach, które z pozoru nie powinny być zaburzone. Efekt ten jest bliżej omówiony w rozdziale Aliasing.
Sygnał dyskretny jako wektor
Skoro sygnał to po prostu ciąg liczb, możemy go potraktować jak wektor. Na płaszczyźnie wektor to para współrzędnych (x, y), w przestrzeni trójwymiarowej trójka liczby (x, y, z), które wyobrażamy sobie jako strzałkę wiodącą od punktu (0, 0, 0) do (x, y, z). Sygnał składający się z pięciu punktów będzie wektorem w przestrzeni pięciowymiarowej, więc intuicja "strzałki" dla większości z nas przestaje być użyteczna. Pomimo tego, możemy wciąż korzystać z użytecznych pojęć z dziedziny algebry wektorów, jak ortogonalność czy iloczyn skalarny.
Iloczyn skalarny
Iloczyn skalarny przyjmiemy jako miarę podobieństwa dwóch sygnałów. Obliczać go będziemy tak samo jak dla wektorów — przypomnijmy: niech [math]\mathbf{x} = [x_1, x_2, x_3][/math], i [math]\mathbf{y} = [y_1, y_2, y_3][/math]; iloczyn skalarny tych wektorów oznaczamy [math]\mathbf x \cdot \mathbf y[/math] (zarówno wytłuszczenie symboli wektorów, jak i symbol mnożenia/ilocznu skalarnego "[math]\cdot[/math]", będziemy dalej pomijać):
[math]\displaystyle \mathbf a \cdot \mathbf b = \sum_{i=1}^3 x_i y_i = x_1 y_1 + x_2 y_2 + x_3 y_3[/math]
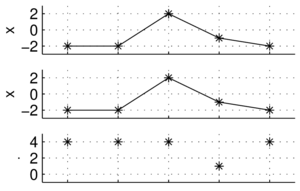
A jak to będzie wyglądać dla sygnałów złożonych z więcej niż trzech punktów? Weźmy
[math]x=[-2, -2, 2, -1, -2][/math]
[math]y=[-1, -1, 1, 1, 0][/math]
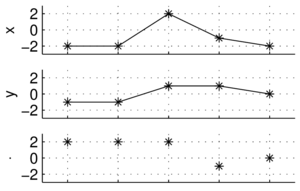
Zamiast strzałek w pięciowymiarowej przestrzeni, łatwiej wizualizować na wykresach wartości kolejnych próbek:
[math]x\cdot y = [-2, -2, 2, -1, -2] \cdot [-1, -1, 1, 1, 0] = 2+2+2-1+0 = 5[/math]
Ortogonalność
Kolejnym użytecznym pojęciem, które możemy zaczerpnąć bezpośrednio z algebry wektorów, jest ortogonalność. Dwa wektory (sygnały) są do siebie ortogonalne, jeśli ich iloczyn skalarny wynosi zero, jak poniżej:
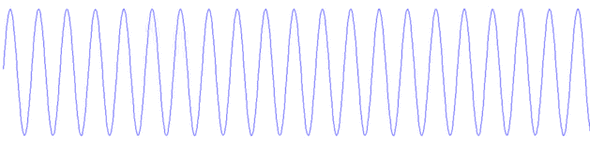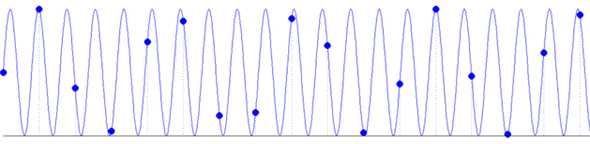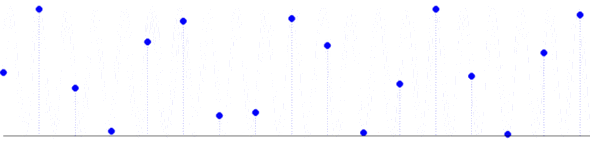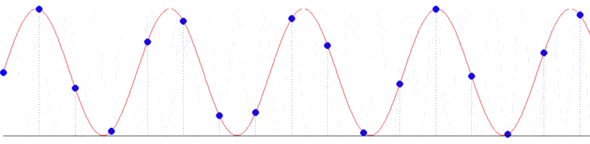
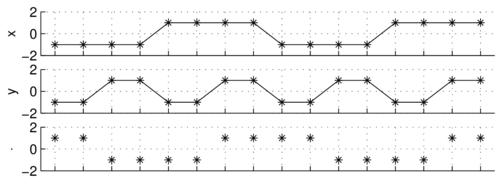
W przypadku sygnału złożonego z 16 punktów, możemy ten fakt sprawdzić obliczając iloczyn skalarny punkt po punkcie, albo też zauważając prawidłowości występujące w każdym okresie górnego sygnału. W przypadku dłuższych i bardziej złożonych sygnałów może to już nie być takie oczywiste, jak np. ortogonalność wszystkich sinusów na poniższym rysunku, których częstości są całkowitymi wielokrotnościami częstości podstawowej:
| Zbiór ortogonalnych sinusów |
| [math]f(x)=\sin(kx), k=1,2,\ldots[/math] |
Energia sygnału
Matematycznie energia sygnału [math]x[/math] to [math]\langle x,x \rangle[/math] (czyli [math]x\cdot x[/math], iloczyn skalarny sygnału "z samym sobą"). Dla sygnałów ciągłych [math]\langle x(t), x(t) \rangle = \int |x(t)|^2 dt[/math], dla sygnałów dyskretnych [math] \langle x[n], x[n] \rangle = \sum_n |x[n]|^2[/math]. Fizycznie musimy wziąć pod uwagę wspomniane wcześniej stałą kalibracji i częstość próbkowania:
- Jeśli sygnałem będzie prąd elektryczny o natężeniu [math]i(t)[/math] mierzonym w amperach, płynący w obwodzie o oporności [math]R[/math] omów, to wytracana przez niego energia wyniesie [math]E_i = R \int |i(t)|^2 dt[/math] dżuli.
- W przypadku sygnału dyskretnego [math]x[t][/math], całkę [math]\int x(t) dt [/math] zastępujemy sumą pól kolejnych prostokątów o wysokości [math]x[n][/math] i szerokości równej odstępowi między kolejnymi punktami [math]\Delta t = \frac{1}{f_s}[/math]
- [math]E_{x[n]} = \Delta t \sum_n |x(n)|^2 = \frac{1}{f_s} \sum_n |x(n)|^2 [/math]
Liczby zespolone
Przypomnijmy w skrócie: [math]i^2=-1[/math]. Liczbę zespoloną [math]z[/math] możemy zapisać w postaci algebraicznej jako
- [math]z=a+bi,[/math]
gdzie [math]a[/math] to część rzeczywista, [math]b[/math] — część urojona.
Sprzężenie zespolone liczby [math]z[/math] oznaczamy [math]\overline{z}[/math]:
- [math]\overline{z} = a - bi[/math]
a jej moduł to [math]|z| = \sqrt{a^2 + b^2}[/math] (inaczej [math]|z| = z \cdot \overline{z}[/math]).
Postać trygonometryczna:
- [math]z = a + bi = |z| \cdot \dfrac{a}{|z|} + |z| \cdot \dfrac{b}{|z|}i = |z| \cdot (\cos \phi + i\sin \phi).[/math]
Wykorzystując wzór Eulera[1]
- [math]e^{i\phi} = \cos(\phi) + i\sin(\phi)[/math]
możemy liczbę zespoloną zapisać jako
- [math]z = |z|e^{i\phi}[/math]
Szereg Fouriera
Sygnał okresowy (o okresie [math]T[/math]) można przedstawić w postaci szeregu Fouriera:
gdzie
| Dowód powyższego wzoru: |
| Mnożymy obie strony równania 1 przez [math]e^\frac{2\pi i k t}{T}[/math]
i całkujemy po [math]dt[/math] od [math]0[/math] do [math]T[/math]: [math] \int_0^T s(t) e^{{{2\pi i k t}\over{T}}} dt = \sum_{n=-\infty}^{+\infty} \int_0^T c_n e^{i{{2 \pi (k-n)}\over{T}} t}dt [/math] Całki po prawej stronie znikają dla [math]k \ne n[/math]. Jedyny niezerowy wyraz dla [math]k = n[/math] wynosi [math]\int_0^T c_n dt[/math], czyli [math]c_n T[/math] (bo [math]e^0=1[/math]). |
Każdą funkcję okresową możemy przedstawić w postaci sumy sinusów i kosinusów z odpowiednimi wagami — przypomnijmy: [math]e^{i \phi} = \cos(\phi) + i \sin(\phi)[/math].
Wagi [math]c_n[/math] możemy traktować jako względny udział odpowiadających im częstości.
Przykład: szereg Fouriera dla prostokąta
Policzmy postać współczynników Fouriera dla funkcji [math]\Theta(t)[/math], określonej na przedziale [math][0,1][/math] w następujący sposób:
- [math] \Theta(t) = \left\{ \begin{matrix} 1 &, & t \in [0, \frac{1}{2})\\ 0 &, & t \in [ \frac{1}{2}, 1] \end{matrix} \right. [/math]
| obliczenia: |
| Bezpośrednio z wzoru 2 dostajemy (dla [math]T = 1[/math])
[math]\begin{matrix}
c_{n} = \frac{1}{T}\int_{0}^{T} \Theta(t) e^\frac{i 2\pi n t}{T} d t
= \int_{0}^\frac{1}{2} e^{{{i 2\pi n t}}} d t = ( \mathrm{dla}\; n \ne 0 ) =
\left [\frac{1}{i 2\pi n} e^{{i 2\pi n t}} \right ]_{t=0}^{t=\frac{1}{2}} \\
= \frac{1}{i 2\pi n} ( e^{i \pi n} - 1 ) =
\left\{
\begin{matrix}
0 & \mathrm{dla}\; n = \pm2, \pm4, \ldots\\
i/\pi n & \mathrm{dla}\; n = \pm1, \pm3, \ldots
\end{matrix}
\right .\\
(\mathrm{dla}\; n=0) \;\; c_0 = \int_{0}^\frac{1}{2} 1 d t = \frac{1}{2}
\end{matrix}[/math]
Tak więc z wzoru 1 [math]\begin{matrix} \Theta(t) = \sum_{-\infty}^{\infty} c_n e^{-i 2 \pi t n} = \frac{1}{2}\; + \sum_{n=\pm1, \pm3, \ldots} \frac{i}{\pi n} e^{-i 2 \pi t n}= \\ = \frac{1}{2}\; + \sum_{n=\pm1, \pm3, \ldots} \frac{i}{\pi n} \left( \cos(2\pi n t) - i \sin( 2\pi n t) \right)=\\ = \frac{1}{2}\; + \sum_{n=\pm1, \pm3, \ldots} \frac{i}{\pi n} \cos(2\pi n t)\;\; + \sum_{n=\pm1, \pm3, \ldots} \frac{1}{\pi n} \sin( 2\pi n t) \end{matrix}[/math]
|
Dostajemy
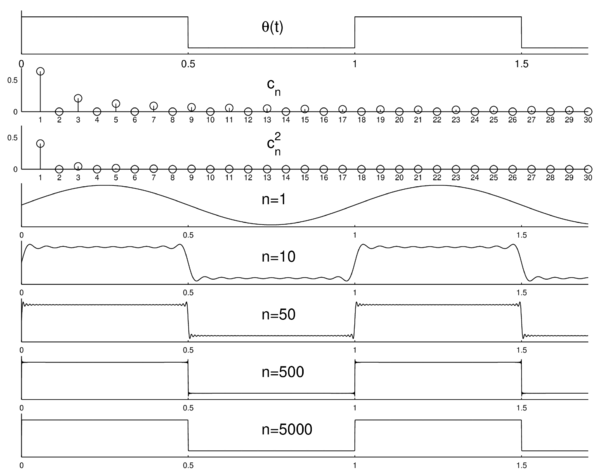
Od góry, kolejno:
funkcja [math]\Theta[/math] (równanie 3) uzupełniona do funkcji okresowej, pierwszych 30 współczynników szeregu Fouriera,
kwadraty współczynników szeregu Fouriera — dyskretne widmo,
pierwszy wyraz rozwinięcia Fouriera, sumy pierwszych 10, 50, 500 i 5000 wyrazów rozwinięcia 4.
Jak widać, najtrudniejsza do wyrażenia z pomocą funkcji
trygonometrycznych jest nieciągłość funkcji [math]\theta(t)[/math] w punktach [math]\left\{\pm \frac{k}{2}, k \in N \right\}[/math]; niejednorodna
zbieżność szeregów Fouriera w tych rejonach nosi nazwę efektu Gibbsa.
Przekształcenie Fouriera
Przejdźmy do nieskończoności z okresem sygnału: [math]T\rightarrow\infty[/math]. Wtedy odstęp [math]\left(\frac{2\pi}{T}\right)[/math] między częstościami kolejnych elementów sumy szeregu Fouriera
[math]\displaystyle s(t) =\sum_{n=-\infty}^{+\infty} c_n e^{-i\frac{2\pi t}{T} n}, [/math]
dąży do [math]0[/math] i suma przechodzi w całkę
funkcja [math]\hat{s}(f)[/math], zastępująca dyskretny ciąg współczynników szeregu Fouriera
[math]\displaystyle c_{n} = \frac{1}{T}\int_{0}^{T} s(t) e^\frac{2\pi i n t}{T} d t [/math]
to transformata Fouriera sygnału [math]s(t)[/math], czyli wynik działania przekształcenia (transformacji) Fouriera [math]\mathcal{F}[/math].
- ↑ wzorem Eulera bywa również nazywane równanie [math]e^{i\pi}+1=0[/math]