Funkcja systemu: Różnice pomiędzy wersjami

Z Brain-wiki
 
(Nie pokazano 99 pośrednich wersji utworzonych przez tego samego użytkownika)
Linia 1: Linia 1:
−
=[[Analiza_sygnałów_-_lecture|AS/]] Funkcja systemu=
+
=[[Analiza_sygnałów_-_lecture|AS/]] Transformacja <math>\mathcal{Z}</math> i widmo procesu AR=
  
 +
=Transformacja <math>\mathcal{Z}</math>=
 +
Jednostronna transformata <math>\mathcal{Z}</math> ciągu liczb <math>x[n]</math> definiowana jest jako funkcja zmiennej <math>z</math> będąca sumą szeregu
  
 +
:<math>
 +
\displaystyle
 +
\mathcal{Z}\{x[n]\} = X(z)= \sum_{n=0}^{\infty} x[n] z^{-n}
 +
</math>
  
 +
czyli np.
 +
<math>
 +
\mathcal{Z}\{(2, 7, 3)\} = 2 z + 7 z^{-1} + 3 z^{-2}
 +
</math>
  
−
==Transformata Z==
 
  
−
(jednostronna) definiowana jest jako szereg
 
−
:<math>\mathcal{Z}\{x[n]\} = X(z)= \sum_{n=0}^{\infty} x[n] z^{-n}</math>
 
−
Dla <math>z=e^{i \omega}</math> dostajemy Dyskretną Transformatę Fouriera.
 
  
−
Transformata <math>\mathcal{Z}</math> jest liniowa
+
Dla <math>z=e^{i \omega}</math> dostajemy Dyskretną Transformację Fouriera.
  
−
:<math>\mathcal{Z}\lbrace a x[n] + b y[n]\rbrace =a X[z] + b Y[z]</math>
+
:<math>
 +
\displaystyle
 +
X(z=e^{i \omega})= \sum_{n=0}^{\infty} x[n] e^{- i \omega n}
 +
</math>
  
−
a dla przesunięcia w czasie
 
  
−
:<math>\mathcal{Z}\lbrace x[n-k]\rbrace  = z^{-k}X(z)</math>
+
Transformacja <math>\mathcal{Z}</math> jest liniowa
  
−
Dowód:
+
:<math>
−
 
+
\displaystyle
−
:<math>\mathcal{Z}\lbrace x[n-k]\rbrace = \sum_{n=0}^{\infty} x[n-k] z^{-n}
+
\mathcal{Z}\lbrace a x[n] + b y[n]\rbrace =a X[z] + b Y[z]
 
</math>
 
</math>
  
−
:<math> | j=n-k|</math>
 
  
−
:<math> = \sum_{j=-k}^{\infty} x[j] z^{-(j+k)} = \sum_{j=-k}^{\infty} x[j] z^{-j}z^{-k}} = z^{-k} \sum_{j=-k}^{\infty} x[j] z^{-j}}  </math>
+
a dla przesunięcia w czasie
−
 
 
−
dla systemów przyczynowych <math>x[j]</math> są niezerowe dla <math>j>0</math>, więc
 
−
 
 
−
:<math>\mathcal{Z}\lbrace x[n-k]\rbrace = z^{-k} \sum_{j=0}^{\infty} x[j] z^{-j}}</math>
 
−
 
 
−
==Widmo procesu AR==
 
  
 
:<math>
 
:<math>
−
x[n] = \sum_{i=1}^M a_i x[n-i] + \epsilon[n]
+
\displaystyle
 +
\mathcal{Z}\lbrace x[n-k]\rbrace  = z^{-k}X(z)
 
</math>
 
</math>
  
−
lub prościej
 
  
−
<math>
+
Dowód:
−
\sum_{i=0}^M a_i x[n-i] = \epsilon[n]
+
 
 +
:::<math>
 +
\displaystyle
 +
\mathcal{Z}\lbrace x[n-k]\rbrace = \sum_{n=0}^{\infty} x[n-k] z^{-n} \;\; \stackrel{ j \rightarrow n-k }{=} \;\;
 +
\sum_{j=-k}^{\infty} x[j] z^{-(j+k)} =
 
</math>
 
</math>
  
−
biorąc transformatę Z obu stron
+
:::<math>
 +
\displaystyle
 +
= \sum_{j=-k}^{\infty} x[j] z^{-j} z^{-k} = z^{-k} \sum_{j=-k}^{\infty} x[j] z^{-j} </math>
  
−
<math>
 
−
\mathcal{Z}\left\{\sum_{i=0}^M a_i x[n-i] \right\}  = \mathcal{Z}\left\{ \epsilon[n] \right\}
 
−
</math>
 
  
−
dostajemy
+
dla systemów przyczynowych <math>x[j]</math> są niezerowe dla <math>j>0</math> (por. [https://brain.fuw.edu.pl/edu/index.php/Systemy_liniowe_niezmiennicze_w_czasie_(LTI)#Splot_i_przyczynowo.C5.9B.C4.87 LTI/Splot i przyczynowość])
 +
więc
  
−
<math>
 
−
A(z) X(z) = E(z)
 
−
</math>
 
  
−
<math>
+
:<math>\displaystyle
−
X(z) = A^{-1}(z) E(z)
+
\mathcal{Z}\lbrace x[n-k]\rbrace = z^{-k} \sum_{j=0}^{\infty} x[j] z^{-j}
 
</math>
 
</math>
  
−
oznaczając <math>A^{-1}(z) = H(z)</math> dostajemy
+
==Transformata <math>\mathcal{Z}</math> splotu==
 +
Niech <math>x[n]=x_1[n]*x_2[n]</math>; wtedy transformata <math>\mathcal{Z}</math> splotu to iloczyn transformat <math>\mathcal{Z}</math>:
  
−
<math>
 
−
X(z) = H(z) E(z)
 
−
</math>
 
  
−
podstawiając <math>z=e^{i\omega t}</math>  przechodzimy z transformaty <math>\mathcal{Z}</math> do transformaty Fouriera:
+
::<math>  
 +
\displaystyle
 +
\mathcal{Z}\{x[n]\} = X(z) = \mathcal{Z}\{x_1[n]\} \mathcal{Z}\{x_2[n]\} = X_1(z)  X_2(z)
 +
</math>  
  
−
<math>
 
−
\hat{x}(\omega) = H(\omega) E(\omega)
 
−
</math>
 
  
−
widmo to kwadrat modułu transformaty Fouriera
+
Dowód:
  
−
<math>
+
:::<math> \displaystyle \mathcal{Z}\{x_1(n)*x_2(n)\} = X(z) = </math>
−
\left| \hat{x}(\omega) \right|^2 = \left| H(\omega) E(\omega) \right|^2 = \left| H(\omega) \right|^2 \sigma^2 = \dfrac{\sigma^2}\left| {A(e^{-i\omega n})} \right|^2
 
−
</math>
 
  
−
gdzie <math>\sigma^2</math> to wariancja nieskorelowanego szumu <math>\epsilon</math>, którego widmo jest płaskie (nie zależy od częstości)
+
:::<math> \displaystyle \sum_{n=-\infty}^\infty\left[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)\right]z^{-n}</math>
  
−
==Procesy ARMA==
+
:::<math>= \displaystyle \sum_{k = -\infty}^\infty x_1(k)\left[\sum_{n=-\infty}^\infty x_2(n-k)z^{-n}\right]</math>
  
−
Przykładem systemów liniowych niezmienniczych w czasie są systemy opisane równaniem
+
:::<math>= \displaystyle \sum_{k = -\infty}^\infty x_1(k)\left[\sum_{n = -\infty}^\infty x_2(n-k)z^{-(n-k)}z^{-k}\right]
−
:<math>
 
−
\sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l]
 
 
</math>
 
</math>
  
−
Jest to ogólna postać procesu ARMA -- autoregressive moving average.
 
  
 +
:::niech <math>n-k = l</math>
  
−
Dla <math>L=0</math> dostajemy proces AR (autoregressive), w którym sygnał na wyjściu <math>y</math> zależy tylko od <math>K</math> poprzednich próbek wyjścia <math>y</math>.
+
:::<math> \displaystyle X(z) = \sum_{k = -\infty}^\infty x_1(k)\left[z^{-k}\sum_{l=-\infty}^\infty x_2(l)z^{-l}\right]</math>
  
 +
:::<math>= \displaystyle \sum_{k = -\infty}^\infty x_1(k) z^{-k} X_2(z)</math>
  
−
Kładąc <math>K=0</math> dostajemy proces MA (moving average), w którym sygnał na wyjściu <math>y</math> zależy tylko od <math>L</math> poprzednich próbek wejścia <math>x</math>.
+
:::<math>= \displaystyle X_1(z) X_2(z) </math>
 +
 
 +
=Widmo procesu AR=
 +
kładąc <math> a_0 = 1</math>, proces AR o znanych współczynnikach <math>a_i</math>
 +
:<math>
 +
\displaystyle
 +
x[n] = \sum_{i=1}^M a_i x[n-i] + \epsilon[n]
 +
</math>
  
−
==Funkcja systemu==
+
możemy zapisać jako
  
−
Zastosujmy do obu stron powyższego równania transformatę<math>\mathcal{Z}</math>:
 
 
:<math>
 
:<math>
−
\mathcal{Z}\left\{\sum_{k=0}^K a_k y[n-k] \right\}  = \mathcal{Z}\left\{ \sum_{l=0}^L b_l x[n-l] \right\}
+
\displaystyle
 +
\sum_{i=0}^M a_i x[n-i] = \epsilon[n]
 
</math>
 
</math>
 +
 +
Biorąc transformatę Z obu stron
  
 
:<math>
 
:<math>
−
\sum_{k=0}^K a_k \mathcal{Z}\left\{ y[n-k]\right\} = \sum_{l=0}^L b_l \mathcal{Z} \left\{x[n-l]\right\}
+
\displaystyle
 +
\mathcal{Z}\left\{\sum_{i=0}^M a_i x[n-i] \right\} = \mathcal{Z}\left\{ \epsilon[n] \right\}
 
</math>
 
</math>
  
−
:<math>
+
 
−
\sum_{k=0}^K a_k z^{-k} Y(z) = \sum_{l=0}^L b_l z^{-l} X(z)
+
dostajemy
 +
 
 +
<math>
 +
A(z) X(z) = E(z)
 
</math>
 
</math>
−
:<math>
+
 
−
Y(z) \sum_{k=0}^K a_k z^{-k} = X(z) \sum_{l=0}^L b_l z^{-l}
+
<math>
 +
X(z) =  \dfrac{E(z)}{A(z)}
 
</math>
 
</math>
  
  
−
Dla systemu przyczynowego dostajemy:
+
oznaczając
 +
 
 +
<math>\displaystyle
 +
H(z) \stackrel{def}{=} A^{-1}(z) = \dfrac{1}{\sum a_i z^{-i}}</math>
  
 +
dostajemy
  
−
:<math>
+
<math>
−
\frac{Y(z)}{X(z)} \equiv H(z) = \frac{\sum_{l=0}^L b_l z^{-l}}{\sum_{k=0}^K a_k z^{-k}}
+
X(z) = H(z) E(z) = \dfrac{E(z)}{a_0 + a_1 z^{-1} + a_2 z^{-2} + \ldots}
 
</math>
 
</math>
  
−
<!--
+
 
−
lub
+
podstawiając <math>z=e^{i\omega t}</math>  przechodzimy z transformaty <math>\mathcal{Z}</math> do transformaty Fouriera <math>\mathcal{F}(x) = \hat{x}(\omega)</math>
 +
 
  
 
:<math>
 
:<math>
−
H(z) = \mathrm{const} \frac  {\prod_{l=0}^L \left(1-\frac{d_l}{z}\right) }      {\prod_{k=0}^K \left(1-\frac{c_k}{z}\right) } .
+
\hat{x}(\omega) = H(\omega) E(\omega)
 
</math>
 
</math>
  
−
-->
 
  
−
<math>H(z)</math> &mdash; funkcja systemu ''(system function)'' pozwala spójnie przedstawić działanie systemu LTI/ARMA realizującego filtrowanie  sygnału <math>x</math>:
+
widmo to kwadrat modułu transformaty Fouriera
 +
 
  
−
:<math>Y(z)=H(z) X(z)</math>
+
:<math>
 +
\displaystyle
 +
\left| \hat{x}(\omega) \right| ^2 =  
 +
\left| H(\omega) E(\omega) \right|^2 = \\
 +
\,\;\;\;\;\;\;\;\;\;\; = \left| H(\omega) \right|^2 \sigma^2 = 
 +
\dfrac{\sigma^2}{\left| {A(e^{-i\omega n})} \right|^2} =
 +
\dfrac{\sigma^2}{\left|a_0 + a_1 e^{-i\omega} + a_2 e^{- 2 i\omega} + \ldots \right|^2}
 +
</math>
  
  
 +
gdzie <math>\sigma^2</math> to wariancja nieskorelowanego szumu <math>\epsilon</math>, którego widmo jest płaskie (nie zależy od częstości)
  
 +
==Wielozmienny model AR==
  
 +
[[Model autoregresyjny (AR)|Model AR]] opisuje wartość
 +
sygnału w chwili <math>t</math> jako kombinację liniową jego wartości
 +
w chwilach poprzednich (oraz szumu). W przypadku wielowymiarowym
 +
możemy włączyć do tego opisu wartości wszystkich sygnałów
 +
<math>s_i</math>, czyli wektora
 +
<math>\vec{s}(t)</math>. Wielozmienny model AR (MVAR, multivariate
 +
autoregressive) można wówczas opisać wzorem:
  
  
 +
<math>
 +
\displaystyle
 +
\vec{s}(t)=\sum_{i=1}^p A(i) \vec{s}(t-i) + \vec{\epsilon}(t) ,
 +
</math>
  
−
==Filtry==
 
  
 +
gdzie <math>\vec{\epsilon}(t)</math> będzie wektorem
 +
szumów, zaś <math>A(i)</math> będą macierzami współczynników modelu.
 +
Przechodząc do przestrzeni częstości otrzymamy:
  
−
===Działanie filtru w dziedzinie czasu, typy filtrów===
 
−
Przypomnijmy definicję splotu:    <math>
 
−
(f * g)[n] = \sum_{m = -\infty}^{\infty} f[m] g[n - m]
 
−
</math>
 
−
==== FIR (MA) ====
 
−
Działanie filtru zadanego przez odpowiedź impulsową ''b'' o długości <math>n_b</math> na sygnał ''x'' można zapisać:
 
  
−
:<math>y(n) = (b*x)[n] =b[0]*x[n] + b[1]*x[n-1] + \dots + b[n_b]*x[n-n_b]</math>
+
<math>
 +
\displaystyle
 +
\vec{s}(\omega)=A^{-1}(\omega) \, \vec{\epsilon}(\omega)=H(\omega)\vec{\epsilon}(\omega),
 +
</math>  
  
−
Taki filtr nazywamy filtrem o skończonej odpowiedzi impulsowej (Finite Impulse Responce, FIR), bo odpowiedź na impulsowe wzbudzenie kończy się po <math>n_b</math> próbkach. Inna nazwa to średnia biegnąca (Moving Average, MA).
 
  
−
Dla filtrów FIR współczynniki filtru i odpowiedź impulsowa są takie same.
+
gdzie <math>H(\omega)</math> jest macierzą przejścia.  MVAR jest modelem typu "czarna skrzynka", gdzie na wejściu występują szumy, na wyjściu sygnały, a system jest opisany przez macierz przejścia. Zawiera ona informacje o własnościach widmowych sygnałów i związkach między nimi.
  
−
==== IIR (AR) ====
 
−
Kolejnym typem filtru jest typ przypominający proces autoregresyjny. Operacja splotu działa tu na sekwencji wyjściowej:
 
−
:<math>
 
−
y[n] = x[n] - a[1]*y[n-1] - \dots - a[n_a]*y[n-n_a]
 
−
</math>
 
  
−
Filtr ten nazywany jest filtr rekursywnym lub autoregresyjnym (AR). W ogólności jego odpowiedź impulsowa może być nieskończona.
+
Na podstawie macierzy <math>H(\omega)</math> można obliczyć macierz
 +
gęstości widmowej zawierającą widma mocy dla pojedynczych kanałów jak
 +
również funkcje wzajemnej gęstości mocy pomiędzy kanałami.  Stosując
 +
tego typu podejście, w którym wszystkie sygnały generowane przez
 +
pewien proces są rozpatrywane jednocześnie, można policzyć z macierzy
 +
spektralnej nie tylko koherencje zwykłe pomiędzy dwoma kanałami, ale
 +
również koherencje wielorakie opisujące związek danego kanału z
 +
pozostałymi i koherencje cząstkowe opisujące bezpośrednie związki
 +
między dwoma kanałami po usunięciu wpływu pozostałych kanałów. W
 +
przypadku gdy pewien kanał 1 będzie wpływał na kanały 2 i 3,
 +
obliczając koherencję zwykłą znajdziemy związek między 2 oraz 3,
 +
chociaż nie są one ze sobą bezpośrednio powiązane, natomiast
 +
koherencja cząstkowa nie wykaże związku między nimi.
  
−
====IIR (ARMA) ====
 
−
Najbardziej ogólnym typem jest połączenie dwóch powyższych czyli:
 
−
::<math>
 
−
\begin{array}{ll}
 
−
y[n] = b[0]*x[n] &+ b[1]*x[n-1] + \dots + b[n_b]*x[n-n_b]\\
 
−
&- a[1]*y[n-1] - \dots - a[n_a]*y[n-n_a]
 
−
\end{array}
 
−
</math>
 
−
Tą wersję filtru nazywamy filtrem o nieskończonej odpowiedzi impulsowej (Infinite Impulse Responce IIR) bo potencjalnie raz wzbudzony może dowolnie długo produkować niezerowe wyjście.
 
  
−
'''Rzędem filtru''' nazywamy maksymane opóźnienie w próbkach potrzebne do wytworzenia nowej próbki wyjściowej. Dla filtrów FIR jest on równy liczbie <math> n_b</math>. Dla filtrów IIR jest to większa z liczb <math>n_a, n_b</math>.
+
Macierz <math>H(\omega)</math> jest niesymetryczna, a jej wyrazy
 +
pozadiagonalne są najczęściej stosowanymi estymatami [https://pl.wikipedia.org/wiki/Przyczynowość_w_sensie_Grangera przyczynowości w sensie Grangera] — 
 +
uwzględnienie wcześniejszej informacji zawartej w jednym z sygnałów
 +
zmniejsza błąd predykcji drugiego sygnału. Opierając się na tej
 +
własności zdefiniowano Kierunkową Funkcję Przejścia (DTF, directed
 +
transfer function) jako znormalizowany element pozadiagonalny
 +
<math>H(\omega)</math>.  DTF opisuje kierunek propagacji i skład
 +
widmowy rozchodzących się sygnałów.
  
−
===Działanie filtru w dziedzinie częstości===
 
−
Stosując transformatę <math>Z</math> ([[%C4%86wiczenia_5#Jak_znale.C5.BA.C4.87_A_.E2.80.94_transformata_Z|analogicznie jak dla procesu AR]]) możemy równanie z dziedziny czasu przenieść do dziedziny częstości. Filtrowanie odpowiada przemnożeniu transformaty sygnału przez transformatę funkcji przenoszenia filtru:
 
  
−
::<math>Y[z]=H[z]X[z]=\frac{b[0]+b[1]z^{-1}+\dots +b[n_b]z^{-n_b}}{a[0]+a[1]z^{-1}+\dots +a[n_a]z^{-n_a}}X[z]</math>
+
Otrzymamy w ten sposób całościowy opis zmian wszystkich sygnałów
 +
jednocześnie.  Co ciekawe, obliczona na tej podstawie funkcja
 +
charakteryzująca zależności między sygnałami <math>s_i</math> (funkcja
 +
przejścia) nie jest symetryczna, w przeciwieństwie do
 +
np. korelacji. Dzięki temu może służyć wnioskowaniu nie tylko o sile
 +
zależności między poszczególnymi sygnałami składowymi, ale też o
 +
kierunku przepływu informacji między nimi.  W przybliżeniu odpowiada
 +
to informacji, w którym z sygnałów struktury odpowiadające danej
 +
częstości pojawiają się wcześniej.
  
−
Występująca tu funkcja ''H'' nosi nazwę transmitancja lub funkcja przenoszenia.
+
[[Plik:DTF.png|400px|thumb|center|MVAR w EEG, dzięki uprzejmości Macieja Kamińskiego]]
−
Znając funkcję <math>H</math>  łatwo możemy przewidzieć co się stanie z widmem sygnału po przefiltrowaniu. Weźmy <math> z = e^{i 2\pi  f}</math>. Wówczas transmitancja jest funkcją częstości ''f''. Dla każdej konkretnej częstości <math>f_k</math> przypisuje ona liczbę zespoloną, którą można wyrazić jako <math>A_k e^{i \phi_k}</math>. W dziedzinie częstości sygnał wyrażony jest przez współczynniki Fourierowskie. Dla konkretnej częstości współczynnik taki <math>X_k = |X_k| e^{i \theta_k}</math> (liczba zespolona) mówi z jaką amplitudą i jaką fazą exponens zespolony o danej częstości (<math>z_k = e^{i 2\pi  f_k}</math>) wchodzi w skład sygnału.
 
  
 +
<references/>
  
−
Zatem działanie filtru na sygnał w dziedzinie częstości polega na przemnożeniu składowej sygnału o częstości <math>f_k</math> przez liczbę <math>A_k e^{i \phi_k}</math>:
 
−
:<math>Y(f_k) = A_k e^{i \phi_k} |X_k| e^{i \theta_k} z_k = A_k |X_k| e^{i ( \phi_k +\theta_k)}  e^{i 2\pi  f_k} </math>
 
−
 
−
Zatem w wyniku filtrowania składowa sygnału o danej częstości może zmienić amplitudę i fazę ale co warto zauważyć nie zmienia częstości.
 
  
−
'''Zera i bieguny''' filtra to odpowiednio miejsca zerowe licznika i mianownika funkcji przenoszenia.
 
  
  
−
<references/>
+
<div align="right">
 +
[[Systemy_liniowe_niezmiennicze_w_czasie_(LTI)|⬅]] [[Analiza_sygnałów_-_wykład|⬆]] [[Filtry|⮕]]
 +
</div>

Aktualna wersja na dzień 21:01, 14 lis 2024

AS/ Transformacja [math]\mathcal{Z}[/math] i widmo procesu AR

Transformacja [math]\mathcal{Z}[/math]

Jednostronna transformata [math]\mathcal{Z}[/math] ciągu liczb [math]x[n][/math] definiowana jest jako funkcja zmiennej [math]z[/math] będąca sumą szeregu

[math] \displaystyle \mathcal{Z}\{x[n]\} = X(z)= \sum_{n=0}^{\infty} x[n] z^{-n} [/math]

czyli np. [math] \mathcal{Z}\{(2, 7, 3)\} = 2 z + 7 z^{-1} + 3 z^{-2} [/math]


Dla [math]z=e^{i \omega}[/math] dostajemy Dyskretną Transformację Fouriera.

[math] \displaystyle X(z=e^{i \omega})= \sum_{n=0}^{\infty} x[n] e^{- i \omega n} [/math]


Transformacja [math]\mathcal{Z}[/math] jest liniowa

[math] \displaystyle \mathcal{Z}\lbrace a x[n] + b y[n]\rbrace =a X[z] + b Y[z] [/math]


a dla przesunięcia w czasie

[math] \displaystyle \mathcal{Z}\lbrace x[n-k]\rbrace = z^{-k}X(z) [/math]


Dowód:

[math] \displaystyle \mathcal{Z}\lbrace x[n-k]\rbrace = \sum_{n=0}^{\infty} x[n-k] z^{-n} \;\; \stackrel{ j \rightarrow n-k }{=} \;\; \sum_{j=-k}^{\infty} x[j] z^{-(j+k)} = [/math]
[math] \displaystyle = \sum_{j=-k}^{\infty} x[j] z^{-j} z^{-k} = z^{-k} \sum_{j=-k}^{\infty} x[j] z^{-j} [/math]


dla systemów przyczynowych [math]x[j][/math] są niezerowe dla [math]j\gt 0[/math] (por. LTI/Splot i przyczynowość) więc


[math]\displaystyle \mathcal{Z}\lbrace x[n-k]\rbrace = z^{-k} \sum_{j=0}^{\infty} x[j] z^{-j} [/math]

Transformata [math]\mathcal{Z}[/math] splotu

Niech [math]x[n]=x_1[n]*x_2[n][/math]; wtedy transformata [math]\mathcal{Z}[/math] splotu to iloczyn transformat [math]\mathcal{Z}[/math]:


[math] \displaystyle \mathcal{Z}\{x[n]\} = X(z) = \mathcal{Z}\{x_1[n]\} \mathcal{Z}\{x_2[n]\} = X_1(z) X_2(z) [/math]


Dowód:

[math] \displaystyle \mathcal{Z}\{x_1(n)*x_2(n)\} = X(z) = [/math]
[math] \displaystyle \sum_{n=-\infty}^\infty\left[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)\right]z^{-n}[/math]
[math]= \displaystyle \sum_{k = -\infty}^\infty x_1(k)\left[\sum_{n=-\infty}^\infty x_2(n-k)z^{-n}\right][/math]
[math]= \displaystyle \sum_{k = -\infty}^\infty x_1(k)\left[\sum_{n = -\infty}^\infty x_2(n-k)z^{-(n-k)}z^{-k}\right] [/math]


niech [math]n-k = l[/math]
[math] \displaystyle X(z) = \sum_{k = -\infty}^\infty x_1(k)\left[z^{-k}\sum_{l=-\infty}^\infty x_2(l)z^{-l}\right][/math]
[math]= \displaystyle \sum_{k = -\infty}^\infty x_1(k) z^{-k} X_2(z)[/math]
[math]= \displaystyle X_1(z) X_2(z) [/math]

Widmo procesu AR

kładąc [math] a_0 = 1[/math], proces AR o znanych współczynnikach [math]a_i[/math]

[math] \displaystyle x[n] = \sum_{i=1}^M a_i x[n-i] + \epsilon[n] [/math]

możemy zapisać jako

[math] \displaystyle \sum_{i=0}^M a_i x[n-i] = \epsilon[n] [/math]

Biorąc transformatę Z obu stron

[math] \displaystyle \mathcal{Z}\left\{\sum_{i=0}^M a_i x[n-i] \right\} = \mathcal{Z}\left\{ \epsilon[n] \right\} [/math]


dostajemy

[math] A(z) X(z) = E(z) [/math]

[math] X(z) = \dfrac{E(z)}{A(z)} [/math]


oznaczając

[math]\displaystyle H(z) \stackrel{def}{=} A^{-1}(z) = \dfrac{1}{\sum a_i z^{-i}}[/math]

dostajemy

[math] X(z) = H(z) E(z) = \dfrac{E(z)}{a_0 + a_1 z^{-1} + a_2 z^{-2} + \ldots} [/math]


podstawiając [math]z=e^{i\omega t}[/math] przechodzimy z transformaty [math]\mathcal{Z}[/math] do transformaty Fouriera [math]\mathcal{F}(x) = \hat{x}(\omega)[/math]


[math] \hat{x}(\omega) = H(\omega) E(\omega) [/math]


widmo to kwadrat modułu transformaty Fouriera


[math] \displaystyle \left| \hat{x}(\omega) \right| ^2 = \left| H(\omega) E(\omega) \right|^2 = \\ \,\;\;\;\;\;\;\;\;\;\; = \left| H(\omega) \right|^2 \sigma^2 = \dfrac{\sigma^2}{\left| {A(e^{-i\omega n})} \right|^2} = \dfrac{\sigma^2}{\left|a_0 + a_1 e^{-i\omega} + a_2 e^{- 2 i\omega} + \ldots \right|^2} [/math]


gdzie [math]\sigma^2[/math] to wariancja nieskorelowanego szumu [math]\epsilon[/math], którego widmo jest płaskie (nie zależy od częstości)

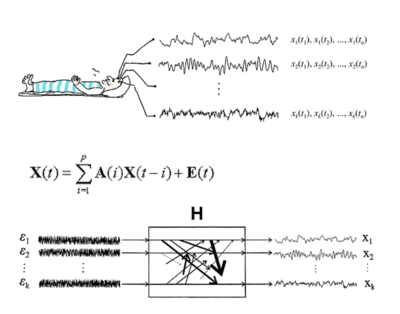
Wielozmienny model AR

Model AR opisuje wartość sygnału w chwili [math]t[/math] jako kombinację liniową jego wartości w chwilach poprzednich (oraz szumu). W przypadku wielowymiarowym możemy włączyć do tego opisu wartości wszystkich sygnałów [math]s_i[/math], czyli wektora [math]\vec{s}(t)[/math]. Wielozmienny model AR (MVAR, multivariate autoregressive) można wówczas opisać wzorem:


[math] \displaystyle \vec{s}(t)=\sum_{i=1}^p A(i) \vec{s}(t-i) + \vec{\epsilon}(t) , [/math]


gdzie [math]\vec{\epsilon}(t)[/math] będzie wektorem szumów, zaś [math]A(i)[/math] będą macierzami współczynników modelu. Przechodząc do przestrzeni częstości otrzymamy:


[math] \displaystyle \vec{s}(\omega)=A^{-1}(\omega) \, \vec{\epsilon}(\omega)=H(\omega)\vec{\epsilon}(\omega), [/math]


gdzie [math]H(\omega)[/math] jest macierzą przejścia. MVAR jest modelem typu "czarna skrzynka", gdzie na wejściu występują szumy, na wyjściu sygnały, a system jest opisany przez macierz przejścia. Zawiera ona informacje o własnościach widmowych sygnałów i związkach między nimi.


Na podstawie macierzy [math]H(\omega)[/math] można obliczyć macierz gęstości widmowej zawierającą widma mocy dla pojedynczych kanałów jak również funkcje wzajemnej gęstości mocy pomiędzy kanałami. Stosując tego typu podejście, w którym wszystkie sygnały generowane przez pewien proces są rozpatrywane jednocześnie, można policzyć z macierzy spektralnej nie tylko koherencje zwykłe pomiędzy dwoma kanałami, ale również koherencje wielorakie opisujące związek danego kanału z pozostałymi i koherencje cząstkowe opisujące bezpośrednie związki między dwoma kanałami po usunięciu wpływu pozostałych kanałów. W przypadku gdy pewien kanał 1 będzie wpływał na kanały 2 i 3, obliczając koherencję zwykłą znajdziemy związek między 2 oraz 3, chociaż nie są one ze sobą bezpośrednio powiązane, natomiast koherencja cząstkowa nie wykaże związku między nimi.


Macierz [math]H(\omega)[/math] jest niesymetryczna, a jej wyrazy pozadiagonalne są najczęściej stosowanymi estymatami przyczynowości w sensie Grangera — uwzględnienie wcześniejszej informacji zawartej w jednym z sygnałów zmniejsza błąd predykcji drugiego sygnału. Opierając się na tej własności zdefiniowano Kierunkową Funkcję Przejścia (DTF, directed transfer function) jako znormalizowany element pozadiagonalny [math]H(\omega)[/math]. DTF opisuje kierunek propagacji i skład widmowy rozchodzących się sygnałów.


Otrzymamy w ten sposób całościowy opis zmian wszystkich sygnałów jednocześnie. Co ciekawe, obliczona na tej podstawie funkcja charakteryzująca zależności między sygnałami [math]s_i[/math] (funkcja przejścia) nie jest symetryczna, w przeciwieństwie do np. korelacji. Dzięki temu może służyć wnioskowaniu nie tylko o sile zależności między poszczególnymi sygnałami składowymi, ale też o kierunku przepływu informacji między nimi. W przybliżeniu odpowiada to informacji, w którym z sygnałów struktury odpowiadające danej częstości pojawiają się wcześniej.

MVAR w EEG, dzięki uprzejmości Macieja Kamińskiego




Źródło: „http://brain.fuw.edu.pl/edu/index.php?title=Funkcja_systemu&oldid=11167”