Filtry: Różnice pomiędzy wersjami

Z Brain-wiki
 
(Nie pokazano 58 pośrednich wersji utworzonych przez tego samego użytkownika)
Linia 8: Linia 8:
 
y[n] = \sum_{k=1}^K a_k y[n-k] + \sum_{l=0}^L b_l x[n-l]
 
y[n] = \sum_{k=1}^K a_k y[n-k] + \sum_{l=0}^L b_l x[n-l]
 
</math>
 
</math>
 +
  
  
Linia 13: Linia 14:
  
  
 +
<div align="center">
 
:<math>
 
:<math>
 
\displaystyle
 
\displaystyle
 
\sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l]
 
\sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l]
 
</math>
 
</math>
 +
</div>
  
−
<!--
 
  
  
−
Jeśli w miejsce sygnału <math>x[n]</math> wstawimy szum <math>\epsilon[i]</math>, dostaniemy równanie opisujące proces ARMA — AutoRegressive Moving Average.
+
==Funkcja przejścia (transfer function)==
 +
 
 +
Zastosujmy do obu stron powyższego równania transformatę <math>\mathcal{Z}</math>:
  
  
 
:<math>
 
:<math>
 
\displaystyle
 
\displaystyle
−
\sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l \epsilon[n-l]
+
\mathcal{Z}\left\{\sum_{k=0}^K a_k y[n-k] \right\}  = \mathcal{Z}\left\{ \sum_{l=0}^L b_l x[n-l] \right\}
 
</math>
 
</math>
  
  
 +
:<math>
 +
\displaystyle
 +
\sum_{k=0}^K a_k \mathcal{Z}\left\{ y[n-k]\right\} = \sum_{l=0}^L b_l \mathcal{Z} \left\{x[n-l]\right\}
 +
</math>
  
−
==Dla <math>L=0</math> dostajemy proces AR (autoregressive)==
 
−
w którym sygnał na wyjściu <math>y</math> zależy tylko od <math>K</math> poprzednich próbek wyjścia <math>y</math>.
 
  
 
:<math>
 
:<math>
 
\displaystyle
 
\displaystyle
−
\epsilon[n] = \sum_{k=0}^K a_k y[n-k]
+
\sum_{k=0}^K a_k z^{-k} Y(z) = \sum_{l=0}^L b_l z^{-l} X(z)
 
</math>
 
</math>
−
 
−
 
−
kładąc <math>a_0 = 1</math>
 
  
  
 
:<math>
 
:<math>
 
\displaystyle
 
\displaystyle
−
\epsilon[n] = y[n] + \sum_{k=1}^K a_k y[n-k]
+
Y(z) \sum_{k=0}^K a_k z^{-k} = X(z) \sum_{l=0}^L b_l z^{-l}
 
</math>
 
</math>
  
  
 +
Dla systemu przyczynowego dostajemy:
 +
 +
<div align="center">
 
:<math>
 
:<math>
 
\displaystyle
 
\displaystyle
−
y[n] = \sum_{k=1}^K -a_k y[n-k] + \epsilon[n]
+
\frac{Y(z)}{X(z)} \equiv H(z) = \frac{\sum_{l=0}^L b_l z^{-l}}{\sum_{k=0}^K a_k z^{-k}}
 
</math>
 
</math>
 +
</div>
 +
 +
==Filtry==
 +
Funkcja przejścia <math>H(z)</math> pozwala zwięźle przedstawić działanie filtra LTI na sygnał <math>x</math> w przestrzeni transformaty <math>\mathcal{Z}</math>:
  
  
 +
::<math>
 +
\displaystyle
 +
Y(z)=H(z)X(z)=\frac{b_0 + b_1 z^{-1}+\dots +b_{L} z^{-L}}{a_0+a_1 z^{-1}+\dots +a_{K} z^{-K}}X(z)
 +
</math>
  
−
==Dla <math>K=0</math> dostajemy proces MA (moving average)==
 
−
w którym sygnał na wyjściu <math>y</math> zależy tylko od <math>L</math> poprzednich próbek wejścia
 
  
 +
gdzie <math>X(z)</math> to transformata <math>\mathcal{Z}</math> filtrowanego sygnału (wejścia <math>x</math>), <math>Y(z)</math> — wyjścia, a <math>H(z)</math> to wprowadzona powyżej funkcja przejścia filtra. Filtrowanie w przestrzeni transformaty <math>\mathcal{Z}</math> odpowiada przemnożeniu transformaty sygnału przez transformatę funkcji przejścia filtru. Analogicznie w przestrzeni częstości — dla <math>z = e^{i\omega}</math> funkcja przejścia zależy od częstości <math>\omega</math>.
  
−
:<math>
+
::<math>
 
\displaystyle
 
\displaystyle
−
y[n] = \sum_{l=0}^L b_l \epsilon[n-l]
+
Y(e^{i\omega})=H(e^{i\omega})X(e^{i\omega})=\frac{b_0+b_1 e^{-i\omega}+\dots +b_L e^{-i L\omega}}{a_0+a_1 e^{-i\omega}+\dots +a_K e^{-i K\omega}}X(e^{i\omega})
 
</math>
 
</math>
  
 +
Działanie funkcji przejścia (czyli filtra) na składową sygnału <math>x</math> o częstości <math>\omega_k</math>, przedstawioną we współrzędnych biegunowych jako  <math>|X_k| e^{i (\omega_k t + \theta_k)}</math>, odpowiada wymnożeniu jej przez liczbę zespoloną <math>H(e^{i\phi_k})</math>, którą również można przedstawić we współrzędnych biegunowych, jako <math>|A_k| e^{i \phi_k}</math>:
  
−
czyli splot szumu <math>\epsilon[n]</math> z sekwencją <math>b_l</math>
+
:<math>Y(\omega_k) = |A_k| e^{i \phi_k} |X_k| e^{i (\omega t + \theta_k)} = |A_k| |X_k| e^{i ( \phi_k +\theta_k)} e^{i \omega t} </math>
 +
 +
W wyniku filtrowania sinusoidalna składowa sygnału o danej częstości może zmienić amplitudę i fazę, ale nie zmienia częstości.
 +
<!--Zera i bieguny filtra to odpowiednio miejsca zerowe licznika i mianownika funkcji przenoszenia.-->
  
−
-->
 
  
−
==Funkcja przejścia (transfer function)==
 
−
 
−
Zastosujmy do obu stron powyższego równania transformatę <math>\mathcal{Z}</math>:
 
  
 +
===Finite Impulse Response (FIR) — filtr o skończonej odpowiedzi impulsowej===
  
 +
Jeśli w równaniu
 +
:<math>
 +
\displaystyle
 +
\sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l]
 +
</math>
 +
położymy <math>a_i = 0</math> poza <math>a_0=1</math>, dostaniemy
 
:<math>
 
:<math>
 
\displaystyle
 
\displaystyle
−
\mathcal{Z}\left\{\sum_{k=0}^K a_k y[n-k] \right\}  = \mathcal{Z}\left\{ \sum_{l=0}^L b_l x[n-l] \right\}
+
y[n] = \sum_{l=0}^L b_l x[n-l]
 
</math>
 
</math>
  
 +
W funkcji przejścia mianownik będzie stały i dostaniemy
  
−
:<math>
+
<math>
 
\displaystyle
 
\displaystyle
−
\sum_{k=0}^K a_k \mathcal{Z}\left\{ y[n-k]\right\} = \sum_{l=0}^L b_l \mathcal{Z} \left\{x[n-l]\right\}
+
Y[z]=H[z]X[z]=\left(b_0+b_1 z^{-1}+\dots +b_L z^{-L}\right) X[z]
 
</math>
 
</math>
  
  
 +
a w dziedzienie czasu, z pełnego równania
 
:<math>
 
:<math>
 
\displaystyle
 
\displaystyle
−
\sum_{k=0}^K a_k z^{-k} Y(z) = \sum_{l=0}^L b_l z^{-l} X(z)
+
y[n] = b_0 x[n]+ b_1 x[n-1] + \dots + b_L x[n-L]
 +
\,\,\, - \,\,\,
 +
a_1 y[n-1] - \dots - a_K y[n-K]
 
</math>
 
</math>
  
 +
pozostaje
  
 
:<math>
 
:<math>
 
\displaystyle
 
\displaystyle
−
Y(z) \sum_{k=0}^K a_k z^{-k} = X(z) \sum_{l=0}^L b_l z^{-l}
+
y(n) = b_0 *x[n] + b_1 *x[n-1] + \dots + b_L *x[n-L]
 
</math>
 
</math>
  
  
−
Dla systemu przyczynowego dostajemy:
+
Jeśli współczynniki <math>b_i</math> zapiszemy jako sekwencję <math>b[i]</math>, zobaczymy, że działanie takiego filtra na sygnał <math>x[n]</math> w dziedzinie czasu jest splotem sekwencji współczynników filtra z sygnałem:
  
  
 
:<math>
 
:<math>
 
\displaystyle
 
\displaystyle
−
\frac{Y(z)}{X(z)} \equiv H(z) = \frac{\sum_{l=0}^L b_l z^{-l}}{\sum_{k=0}^K a_k z^{-k}}
+
y(n) = b[0]*x[n] + b[1]*x[n-1] + \dots + b[L]*x[n-L] = b[n]*x[n]
 
</math>
 
</math>
  
  
−
<math>H(z)</math> &mdash; funkcja systemu ''(system function)'' pozwala spójnie przedstawić działanie filtra LTI na sygnał <math>x</math> w przestrzeni transformaty <math>\mathcal{Z}</math>:
+
Taki filtr nazywamy filtrem o skończonej odpowiedzi impulsowej (Finite Impulse Response, FIR), bo odpowiedź na impuls  kończy się po <math>L</math> próbkach. Inna nazwa to średnia biegnąca (Moving Average, MA).
 +
 
 +
 
 +
 
 +
===Infinite Impulse Response (IIR) — filtr o nieskończonej odpowiedzi impulsowej===
 +
Jeśli w równaniu
 +
:<math>
 +
\displaystyle
 +
\sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l]
 +
</math>
 +
położymy <math>b_i = 0</math> poza <math>b_0=1</math>, dostaniemy
 +
:<math>
 +
\displaystyle
 +
\sum_{k=0}^K a_k y[n-k] = x[n]
 +
</math>
  
 +
w funkcji przejścia licznik będzie stały
  
 
::<math>
 
::<math>
 
\displaystyle
 
\displaystyle
−
Y[z]=H[z]X[z]=\frac{b_0 + b_1 z^{-1}+\dots +b_{L} z^{-L}}{a_0+a_1 z^{-1}+\dots +a_{K} z^{-K}}X[z]
+
Y[z]=H[z]X[z]=\frac{1}{a_0+a_1 z^{-1}+\dots +a_{K} z^{-K}}X[z]
 
</math>
 
</math>
  
  
−
W dziedzienie czasu mamy
+
Operacja splotu działa tu na sekwencji wyjściowej:
 +
:<math>
 +
y[n] = x[n] - a[1]*y[n-1] - \dots - a[n_a]*y[n-K]
 +
</math>
  
 +
dlatego taki filtr nazwać można filtrem rekursywnym, autoregresyjnym (AR), lub
 +
filtrem o nieskończonej odpowiedzi impulsowej (Infinite Impulse Response IIR), bo potencjalnie raz wzbudzony (sekwencją jednostkową) może dowolnie długo produkować niezerowe wyjście.
 +
Faza filtrowanego sygnału zaburzana jest nieliniowo ('''nonlinear phase filter''').
 +
 +
<!--
 +
Filtry IIR mogą być też implementowane jako połączenie członów AR i MA, czyli:
  
 
::<math>
 
::<math>
−
\displaystyle
+
\begin{array}{ll}
−
\begin{array}{rl}
+
y[n] = b[0]*x[n] &+ b[1]*x[n-1] + \dots + b[L]*x[n-L]\\
−
y[n] = &b_0 x[n]+ b_1 x[n-1] + \dots + b_L x[n-L]\\
+
&- a[1]*y[n-1] - \dots - a[K]*y[n-K]
−
&- a_1 y[n-1] - \dots - a_K y[n-K]
 
 
\end{array}
 
\end{array}
 
</math>
 
</math>
 +
-->
  
 +
==Liniowe i nieliniowe opóźnienie fazy, opóźnienie grupowe==
 +
Jak ustaliliśmy powyżej, filtry liniowe odpowiadają mnożeniu poszczególnych składowych sygnału wejściowego <math>x[n]</math> przez liczbę zespoloną, mającą charakterystyczną dla danego filtra amplitudę i fazę, które dla każdej częstości <math>\omega</math> można wyliczyć z funkcji przenoszenia <math>H(\omega)</math>.
  
−
==Finite Impulse Response (FIR) — filtr o skończonej odpowiedzi impulsowej==
+
Różna dla różnych częstości zmiana amplitudy jest kwintesencją i celem całego procesu filtrowania, w którym z sygnału usuwamy (w praktyce raczej osłabiamy) niechciane częstości.
 +
Jednak wywołana tym procesem zmiana faz dla różnych częstości nie jest już tak oczywista. Weźmy sygnał złożony z dwóch oscylacji, o częstościach <math>\omega</math> i <math>2 *\omega</math>:
  
−
[[Plik:Phase1.png|width=800|bezramki|prawo]]
+
<div align="center">
−
[[Plik:Phase2.png|bezramki|width=800|prawo]]
+
:<math>x(t) = \sin(\omega t) + \sin(2 * \omega t)</math>
−
[[Plik:Phase3.png|bezramki|width=800|prawo]]
+
</div>
  
−
Jeśli w równaniu
 
−
:<math>
 
−
\displaystyle
 
−
\sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l]
 
−
</math>
 
−
położymy <math>a_i = 0</math> poza <math>a_0=1</math>, dostaniemy
 
−
:<math>
 
−
\displaystyle
 
−
y[n] = \sum_{l=0}^L b_l x[n-l]
 
−
</math>
 
  
−
W funkcji przejścia mianownik będzie stały i dostaniemy
+
Suma tych dwóch składowych (niebieskie krzywe) na poniższym rysunku przedstawiona jest kolorem czerwonym:
 +
 
 +
[[Plik:Phase1.png|500px|center|bezramki]]
 +
 
 +
Przesuńmy teraz fazę obydwu sygnałów składowych o tę samą wartość, na przykład <math>\pi/2</math>, i ponownie dodajmy do siebie. Odpowiada to sytuacji, kiedy po przejściu przez filtr sygnału <math>x(t) = \sin(\omega t) + \sin(2 * \omega t)</math> dostajemy <math>y(t) = \sin(\omega t + \pi/2) + \sin(2 * \omega t + \pi/2)</math>
  
−
<math>
+
[[Plik:Phase1.png|150px|left|bezramki]]
−
\displaystyle
+
[[Plik:Phase2.png|500px|center|bezramki]]
−
Y[z]=H[z]X[z]=\left(b_0+b_1 z^{-1}+\dots +b_L z^{-L}\right) X[z]
 
−
</math>
 
  
  
−
a w dziedzienie czasu  
+
Po przejściu przez system, opóźniający fazę <math>\phi</math> jednolicie (o <math>\Delta\phi=\pi/{2}</math>) dla wszystkich częstości, sygnał wyjściowy wygląda zupełnie inaczej, niż sygnał wejściowy. Przed ponownym "złożeniem" każdy z sygnałów składowych został przesunięty o inny odcinek czasu, który dla częstości <math>\omega</math> wynosi <math>\phi/{\omega}</math>:
  
  
−
:<math>
+
<div align="center">
−
\displaystyle
+
:<math>\displaystyle \sin(\omega t + \phi) = sin\left(\,\,\omega (t + \phi/{\omega}) \,\, \right) =
−
y(n) = b_0 *x[n] + b_1 *x[n-1] + \dots + b_L *x[n-L]
+
\sin\left(\,\, \omega (t + \Delta t)\,\, \right)
 
</math>
 
</math>
 +
</div>
  
  
−
jeśli współczynniki <math>b_i</math> zapiszemy jako <math>b[i]</math>, dostaniemy splot
+
Formalnie, opóźnienie '''fazy''' <math>\phi</math> dla danej częstości <math>\omega</math> określamy mianem '''opóźnienia fazowego''', i definiujemy jako <math>-\phi/\omega</math>.
  
  
−
:<math>
+
Przesunięcie składowej sygnału w czasie zwiemy '''opóźnieniem grupowym''', i definiujemy jako  <math>-\frac{d \phi(\omega)}{d \omega}</math>.
−
\displaystyle
+
 
−
y(n) = b[0]*x[n] + b[1]*x[n-1] + \dots + b[L]*x[n-L] = b[n]*x[n]
+
 
−
</math>
+
Żeby otrzymać sygnał, którego wszystkie składowe będą przesunięte o ten sam odcinek czasu <math>\Delta t</math>, czyli będą miały stałe przesunięcie grupowe, trzeba fazę przesuwać '''liniowo''' w zależności od częstości: <math>\Delta\phi(\omega) = \omega\Delta t</math>, wtedy opóźnienie grupowe <math>\frac{d \phi(\omega)}{d \omega} = \frac{d (\omega\Delta t)}{d \omega} = \Delta t</math> będzie stałe.
  
 +
[[Plik:Phase1.png|150px|left|bezramki]]
 +
[[Plik:Phase3.png|500px|center|bezramki]]
  
  
−
Taki filtr nazywamy filtrem o skończonej odpowiedzi impulsowej (Finite Impulse Response, FIR), bo odpowiedź na impulsowe wzbudzenie kończy się po <math>n_b</math> próbkach. Inna nazwa to średnia biegnąca (Moving Average, MA).
+
W każdym innym przypadku sygnał na wyjściu nie będzie odtwarzał własności fazowych (czyli "kształtu", obserwowanego w dziedzinie czasu) sygnału oryginalnego, nawet w zakresie częstości nie zmienianych w procesie filtrowania — zgadzać się będzie tylko widmo w paśmie przenoszenia.
  
−
<!--
 
−
Dla filtrów FIR współczynniki filtru i odpowiedź impulsowa są takie same.
 
−
-->
 
  
−
''Jeśli współczynniki tworzą sekwencję symetryczną bądź antysymetryczną'', oparty na nich filtr FIR będzie liniowo przesuwał fazę filtrowanego sygnału ('''linear phase filter''') — sygnał filtrowany jest przesunięty w czasie o ok. <math>n_b / 2</math>.
 
  
  
 
{| role="presentation" class="wikitable mw-collapsible mw-collapsed"
 
{| role="presentation" class="wikitable mw-collapsible mw-collapsed"
−
| <strong>kod (uproszczony)</strong>
+
| <strong>kod (uproszczony) </strong>
 
|-
 
|-
 
|<source lang=python>
 
|<source lang=python>
Linia 223: Linia 266:
 
</source>
 
</source>
 
|}
 
|}
 +
{| role="presentation" class="wikitable mw-collapsible mw-collapsed"
 +
| <strong>kod generujący obrazki </strong>
 +
|-
 +
|<source lang=python>
  
−
==Infinite Impulse Response (IIR) —  filtr o nieskończonej odpowiedzi impulsowej==
+
import matplotlib.pyplot as plt
−
Jeśli w równaniu
+
import numpy as np
−
:<math>
 
−
\displaystyle
 
−
\sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l]
 
−
</math>
 
−
położymy <math>b_i = 0</math> poza <math>b_0=1</math>, dostaniemy
 
−
:<math>
 
−
\displaystyle
 
−
\sum_{k=0}^K a_k y[n-k] = x[n]
 
−
</math>
 
  
−
w funkcji przejścia licznik będzie stały
+
t = np.arange(0.0, 3, 0.01)
 +
s1 = np.sin(2 * np.pi * t)
 +
s2 = np.sin(2 * np.pi * t + np.pi / 2)
 +
s3 = np.sin(2 * 2 * np.pi * t)
 +
s4 = np.sin(2 * 2 * np.pi * t + np.pi / 2)
 +
s5 = np.sin(2 * 2 * np.pi * t + 2 * np.pi / 2)
  
−
::<math>
+
def fix_axes():
−
\displaystyle
+
    for i in range(0, 3):
−
Y[z]=H[z]X[z]=\frac{1}{a_0+a_1 z^{-1}+\dots +a_{K} z^{-K}}X[z]
+
        ax[i].set_yticks([0], [])
−
</math>
+
        ax[i].set_xlim([0, 3])
 +
        ax[i].grid(True)
 +
        ax[i].set_frame_on(False)
 +
        ax[i].tick_params(length=0)
 +
        ax[i].set_ylim(-2, 2)
  
 +
fig1, ax = plt.subplots(3, 1, dpi=200)
 +
ax[0].plot(t, s1)
 +
ax[1].plot(t, s3)
 +
ax[2].plot(t, s1 + s3, 'r')
 +
ax[0].set_title('sin( $\omega$t )', loc='left')
 +
ax[1].set_title('sin( 2*$\omega$t )', loc='left')
 +
ax[2].set_title('sin( $\omega$t ) + sin( 2*$\omega$t )', loc='left')
 +
fix_axes()
 +
for i in range(0, 3):
 +
    ax[i].set_xticks(np.arange(.25, 3, 1), [])
 +
plt.show()
  
−
Operacja splotu działa tu na sekwencji wyjściowej:
+
fig2, ax = plt.subplots(3, 1, dpi=200)
−
:<math>
+
ax[0].plot(t, s2)
−
y[n] = x[n] - a[1]*y[n-1] - \dots - a[n_a]*y[n-n_a]
+
ax[1].plot(t, s4)
−
</math>
+
ax[2].plot(t, s2 + s4, 'r')
 +
ax[0].set_title('sin( $\omega$t + $\pi$/2 )', loc='left')
 +
ax[1].set_title('sin( 2*$\omega$t + $\pi/2$ )', loc='left')
 +
ax[2].set_title('sin( $\omega$t + $\pi$/2 ) + sin( 2*$\omega$t + $\pi$/2 )', loc='left')
 +
fix_axes()
 +
for i in range(0, 3):
 +
    ax[i].set_xticks(np.arange(0, 3, 1), [])
 +
plt.show()
  
 +
fig3, ax = plt.subplots(3, 1, dpi=200)
 +
ax[0].plot(t, s2)
 +
ax[1].plot(t, s5)
 +
ax[2].plot(t, s2 + s5, 'r')
 +
ax[0].set_title('sin( $\omega$(t + $\pi$/2) )', loc='left')
 +
ax[1].set_title('sin( 2*$\omega$t + 2*$\pi$/2 )', loc='left')
 +
ax[2].set_title('sin( $\omega$t + $\pi$/2 ) + sin( 2*$\omega$t + 2*$\pi$/2 )', loc='left')
 +
fix_axes()
 +
for i in range(0, 3):
 +
    ax[i].set_xticks(np.arange(0, 3, 1), [])
 +
plt.show()
 +
</source>
 +
|}
  
−
Taki filtr ten nazwać można filtrem rekursywnym lub autoregresyjnym (AR).
 
  
−
W praktyce filtry IIR są zwykle implementowane jako połączenie członów AR i MA, czyli:
+
<div align="right">
−
 
+
  [[Funkcja_systemu|⬅]] [[Analiza_sygnałów_-_wykład|⬆]] [[Spektrogram|⮕]]
−
::<math>
+
</div>
−
\begin{array}{ll}
 
−
y[n] = b[0]*x[n] &+ b[1]*x[n-1] + \dots + b[n_b]*x[n-n_b]\\
 
−
&- a[1]*y[n-1] - \dots - a[n_a]*y[n-n_a]
 
−
\end{array}
 
−
</math>
 
−
 
 
−
Tę wersję filtru nazywamy filtrem o nieskończonej odpowiedzi impulsowej (Infinite Impulse Response IIR) bo potencjalnie raz wzbudzony może dowolnie długo produkować niezerowe wyjście.
 
−
Faza filtrowanego sygnału zaburzana jest nieliniowo ('''nonlinear phase filter''')
 
−
 
 
−
'''Rzędem filtru''' nazywamy maksymane opóźnienie w próbkach potrzebne do wytworzenia nowej próbki wyjściowej. Dla filtrów FIR jest on równy liczbie <math>n_b</math>. Dla filtrów IIR jest to większa z liczb <math>n_a, n_b</math> (w praktyce często <math>n_a=n_b</math>).
 
−
 
 
−
 
 
−
Stosując transformatę <math>Z</math> możemy równanie z dziedziny czasu przenieść do dziedziny częstości. Filtrowanie odpowiada przemnożeniu transformaty sygnału przez transformatę funkcji przenoszenia filtru:
 
−
 
 
−
 
 
−
::<math>
 
−
\displaystyle
 
−
Y[z]=H[z]X[z]=\frac{b[0]+b[1]z^{-1}+\dots +b[n_b]z^{-n_b}}{a[0]+a[1]z^{-1}+\dots +a[n_a]z^{-n_a}}X[z]</math>
 
−
 
 
−
 
 
−
Występująca tu funkcja <math>H(z)</math> nosi nazwę transmitancji lub funkcja przenoszenia.
 
−
Znając funkcję <math>H</math> łatwo możemy przewidzieć co się stanie z widmem sygnału po przefiltrowaniu. Weźmy <math> z = e^{i\omega}</math>. Wówczas transmitancja jest funkcją częstości <math>\omega</math>. Konkretnej częstości <math>\omega_k</math> przypisuje ona liczbę zespoloną, którą można wyrazić jako <math>A_k e^{i \phi_k}</math>.
 
−
 
 
−
::<math>
 
−
\displaystyle
 
−
Y[e^{i\omega}]=H[e^{i\omega}]X[e^{i\omega}]=\frac{b[0]+b[1]e^{-i\omega}+\dots +b[n_b]e^{-i\omega n_b}}{a[0]+a[1]e^{-i\omega}+\dots +a[n_a]e^{-i\omega n_a}}X[e^{i\omega}]
 
−
</math>
 
−
 
 
−
W dziedzinie częstości sygnał wyrażony jest przez współczynniki Fourierowskie. Dla konkretnej częstości współczynnik taki <math>X_k = |X_k| e^{i \theta_k}</math> (liczba zespolona) mówi z jaką amplitudą i jaką fazą exponens zespolony o danej częstości (<math>z_k = e^{i\omega_k}</math>) wchodzi w skład sygnału.
 
−
 
 
−
Działanie filtru na sygnał w dziedzinie częstości polega na przemnożeniu składowej sygnału o częstości <math>f_k</math> przez liczbę <math>A_k e^{i \phi_k}</math>:
 
−
 
 
−
:<math>Y(f_k) = A_k e^{i \phi_k} |X_k| e^{i \theta_k} = A_k |X_k| e^{i ( \phi_k +\theta_k)}  e^{i 2\pi  f_k} </math>
 
−
 
−
W wyniku filtrowania sinusoidalna składowa sygnału o danej częstości może zmienić amplitudę i fazę ale co warto zauważyć nie zmienia częstości.
 
−
Zera i bieguny filtra to odpowiednio miejsca zerowe licznika i mianownika funkcji przenoszenia.
 

Aktualna wersja na dzień 21:18, 14 lis 2024

AS/ Funkcja przejścia i filtry

Cyfrowe filtry liniowe niezmiennicze w czasie [math]x[n] \longrightarrow \boxed{LTI} \longrightarrow y[n][/math] opisuje liniowe równanie różnicowe o stałych współczynnikach


[math] \displaystyle y[n] = \sum_{k=1}^K a_k y[n-k] + \sum_{l=0}^L b_l x[n-l] [/math]


gdzie [math]a_i[/math] i [math]b_i[/math] to współczynniki, [math]x[n][/math] to sygnał wejściowy, a [math]y[n][/math] — wyjście; w ogólniejszej postaci można je zapisać jako


[math] \displaystyle \sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l] [/math]


Funkcja przejścia (transfer function)

Zastosujmy do obu stron powyższego równania transformatę [math]\mathcal{Z}[/math]:


[math] \displaystyle \mathcal{Z}\left\{\sum_{k=0}^K a_k y[n-k] \right\} = \mathcal{Z}\left\{ \sum_{l=0}^L b_l x[n-l] \right\} [/math]


[math] \displaystyle \sum_{k=0}^K a_k \mathcal{Z}\left\{ y[n-k]\right\} = \sum_{l=0}^L b_l \mathcal{Z} \left\{x[n-l]\right\} [/math]


[math] \displaystyle \sum_{k=0}^K a_k z^{-k} Y(z) = \sum_{l=0}^L b_l z^{-l} X(z) [/math]


[math] \displaystyle Y(z) \sum_{k=0}^K a_k z^{-k} = X(z) \sum_{l=0}^L b_l z^{-l} [/math]


Dla systemu przyczynowego dostajemy:

[math] \displaystyle \frac{Y(z)}{X(z)} \equiv H(z) = \frac{\sum_{l=0}^L b_l z^{-l}}{\sum_{k=0}^K a_k z^{-k}} [/math]

Filtry

Funkcja przejścia [math]H(z)[/math] pozwala zwięźle przedstawić działanie filtra LTI na sygnał [math]x[/math] w przestrzeni transformaty [math]\mathcal{Z}[/math]:


[math] \displaystyle Y(z)=H(z)X(z)=\frac{b_0 + b_1 z^{-1}+\dots +b_{L} z^{-L}}{a_0+a_1 z^{-1}+\dots +a_{K} z^{-K}}X(z) [/math]


gdzie [math]X(z)[/math] to transformata [math]\mathcal{Z}[/math] filtrowanego sygnału (wejścia [math]x[/math]), [math]Y(z)[/math] — wyjścia, a [math]H(z)[/math] to wprowadzona powyżej funkcja przejścia filtra. Filtrowanie w przestrzeni transformaty [math]\mathcal{Z}[/math] odpowiada przemnożeniu transformaty sygnału przez transformatę funkcji przejścia filtru. Analogicznie w przestrzeni częstości — dla [math]z = e^{i\omega}[/math] funkcja przejścia zależy od częstości [math]\omega[/math].

[math] \displaystyle Y(e^{i\omega})=H(e^{i\omega})X(e^{i\omega})=\frac{b_0+b_1 e^{-i\omega}+\dots +b_L e^{-i L\omega}}{a_0+a_1 e^{-i\omega}+\dots +a_K e^{-i K\omega}}X(e^{i\omega}) [/math]

Działanie funkcji przejścia (czyli filtra) na składową sygnału [math]x[/math] o częstości [math]\omega_k[/math], przedstawioną we współrzędnych biegunowych jako [math]|X_k| e^{i (\omega_k t + \theta_k)}[/math], odpowiada wymnożeniu jej przez liczbę zespoloną [math]H(e^{i\phi_k})[/math], którą również można przedstawić we współrzędnych biegunowych, jako [math]|A_k| e^{i \phi_k}[/math]:

[math]Y(\omega_k) = |A_k| e^{i \phi_k} |X_k| e^{i (\omega t + \theta_k)} = |A_k| |X_k| e^{i ( \phi_k +\theta_k)} e^{i \omega t} [/math]

W wyniku filtrowania sinusoidalna składowa sygnału o danej częstości może zmienić amplitudę i fazę, ale nie zmienia częstości.


Finite Impulse Response (FIR) — filtr o skończonej odpowiedzi impulsowej

Jeśli w równaniu

[math] \displaystyle \sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l] [/math]

położymy [math]a_i = 0[/math] poza [math]a_0=1[/math], dostaniemy

[math] \displaystyle y[n] = \sum_{l=0}^L b_l x[n-l] [/math]

W funkcji przejścia mianownik będzie stały i dostaniemy

[math] \displaystyle Y[z]=H[z]X[z]=\left(b_0+b_1 z^{-1}+\dots +b_L z^{-L}\right) X[z] [/math]


a w dziedzienie czasu, z pełnego równania

[math] \displaystyle y[n] = b_0 x[n]+ b_1 x[n-1] + \dots + b_L x[n-L] \,\,\, - \,\,\, a_1 y[n-1] - \dots - a_K y[n-K] [/math]

pozostaje

[math] \displaystyle y(n) = b_0 *x[n] + b_1 *x[n-1] + \dots + b_L *x[n-L] [/math]


Jeśli współczynniki [math]b_i[/math] zapiszemy jako sekwencję [math]b[i][/math], zobaczymy, że działanie takiego filtra na sygnał [math]x[n][/math] w dziedzinie czasu jest splotem sekwencji współczynników filtra z sygnałem:


[math] \displaystyle y(n) = b[0]*x[n] + b[1]*x[n-1] + \dots + b[L]*x[n-L] = b[n]*x[n] [/math]


Taki filtr nazywamy filtrem o skończonej odpowiedzi impulsowej (Finite Impulse Response, FIR), bo odpowiedź na impuls kończy się po [math]L[/math] próbkach. Inna nazwa to średnia biegnąca (Moving Average, MA).


Infinite Impulse Response (IIR) — filtr o nieskończonej odpowiedzi impulsowej

Jeśli w równaniu

[math] \displaystyle \sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l] [/math]

położymy [math]b_i = 0[/math] poza [math]b_0=1[/math], dostaniemy

[math] \displaystyle \sum_{k=0}^K a_k y[n-k] = x[n] [/math]

w funkcji przejścia licznik będzie stały

[math] \displaystyle Y[z]=H[z]X[z]=\frac{1}{a_0+a_1 z^{-1}+\dots +a_{K} z^{-K}}X[z] [/math]


Operacja splotu działa tu na sekwencji wyjściowej:

[math] y[n] = x[n] - a[1]*y[n-1] - \dots - a[n_a]*y[n-K] [/math]

dlatego taki filtr nazwać można filtrem rekursywnym, autoregresyjnym (AR), lub filtrem o nieskończonej odpowiedzi impulsowej (Infinite Impulse Response IIR), bo potencjalnie raz wzbudzony (sekwencją jednostkową) może dowolnie długo produkować niezerowe wyjście. Faza filtrowanego sygnału zaburzana jest nieliniowo (nonlinear phase filter).


Liniowe i nieliniowe opóźnienie fazy, opóźnienie grupowe

Jak ustaliliśmy powyżej, filtry liniowe odpowiadają mnożeniu poszczególnych składowych sygnału wejściowego [math]x[n][/math] przez liczbę zespoloną, mającą charakterystyczną dla danego filtra amplitudę i fazę, które dla każdej częstości [math]\omega[/math] można wyliczyć z funkcji przenoszenia [math]H(\omega)[/math].

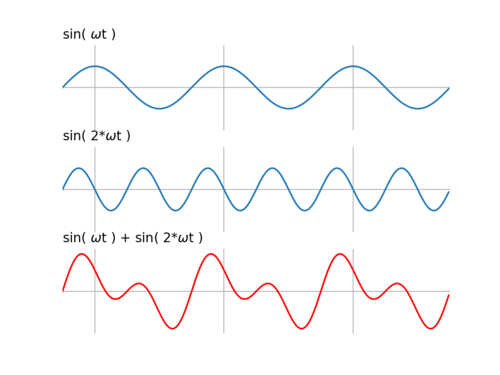
Różna dla różnych częstości zmiana amplitudy jest kwintesencją i celem całego procesu filtrowania, w którym z sygnału usuwamy (w praktyce raczej osłabiamy) niechciane częstości. Jednak wywołana tym procesem zmiana faz dla różnych częstości nie jest już tak oczywista. Weźmy sygnał złożony z dwóch oscylacji, o częstościach [math]\omega[/math] i [math]2 *\omega[/math]:

[math]x(t) = \sin(\omega t) + \sin(2 * \omega t)[/math]


Suma tych dwóch składowych (niebieskie krzywe) na poniższym rysunku przedstawiona jest kolorem czerwonym:

Phase1.png

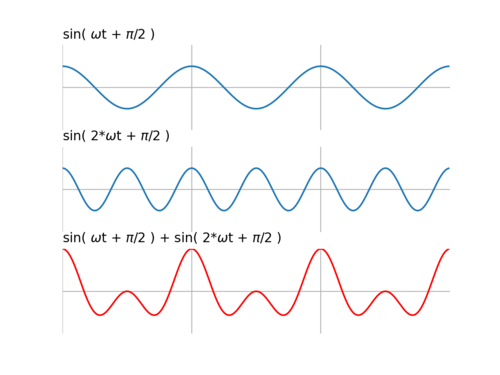
Przesuńmy teraz fazę obydwu sygnałów składowych o tę samą wartość, na przykład [math]\pi/2[/math], i ponownie dodajmy do siebie. Odpowiada to sytuacji, kiedy po przejściu przez filtr sygnału [math]x(t) = \sin(\omega t) + \sin(2 * \omega t)[/math] dostajemy [math]y(t) = \sin(\omega t + \pi/2) + \sin(2 * \omega t + \pi/2)[/math]

Phase1.png
Phase2.png


Po przejściu przez system, opóźniający fazę [math]\phi[/math] jednolicie (o [math]\Delta\phi=\pi/{2}[/math]) dla wszystkich częstości, sygnał wyjściowy wygląda zupełnie inaczej, niż sygnał wejściowy. Przed ponownym "złożeniem" każdy z sygnałów składowych został przesunięty o inny odcinek czasu, który dla częstości [math]\omega[/math] wynosi [math]\phi/{\omega}[/math]:


[math]\displaystyle \sin(\omega t + \phi) = sin\left(\,\,\omega (t + \phi/{\omega}) \,\, \right) = \sin\left(\,\, \omega (t + \Delta t)\,\, \right) [/math]


Formalnie, opóźnienie fazy [math]\phi[/math] dla danej częstości [math]\omega[/math] określamy mianem opóźnienia fazowego, i definiujemy jako [math]-\phi/\omega[/math].


Przesunięcie składowej sygnału w czasie zwiemy opóźnieniem grupowym, i definiujemy jako [math]-\frac{d \phi(\omega)}{d \omega}[/math].


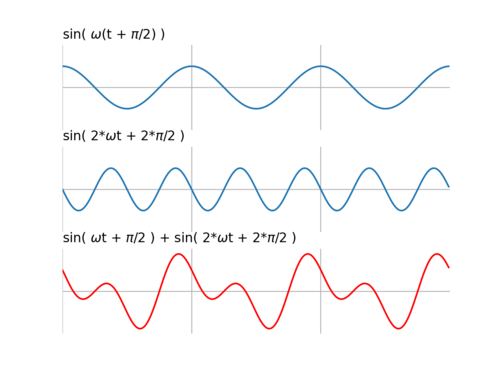
Żeby otrzymać sygnał, którego wszystkie składowe będą przesunięte o ten sam odcinek czasu [math]\Delta t[/math], czyli będą miały stałe przesunięcie grupowe, trzeba fazę przesuwać liniowo w zależności od częstości: [math]\Delta\phi(\omega) = \omega\Delta t[/math], wtedy opóźnienie grupowe [math]\frac{d \phi(\omega)}{d \omega} = \frac{d (\omega\Delta t)}{d \omega} = \Delta t[/math] będzie stałe.

Phase1.png
Phase3.png


W każdym innym przypadku sygnał na wyjściu nie będzie odtwarzał własności fazowych (czyli "kształtu", obserwowanego w dziedzinie czasu) sygnału oryginalnego, nawet w zakresie częstości nie zmienianych w procesie filtrowania — zgadzać się będzie tylko widmo w paśmie przenoszenia.




Źródło: „http://brain.fuw.edu.pl/edu/index.php?title=Filtry&oldid=11168”