Wstep: Różnice pomiędzy wersjami
| Linia 168: | Linia 168: | ||
===Energia sygnału=== | ===Energia sygnału=== | ||
| − | Matematycznie energia sygnału <math>x</math> to <math> | + | Matematycznie energia sygnału <math>x</math> to <math>\langle x,x \rangle</math> (czyli <math>x\cdot x</math>, iloczyn skalarny sygnału "z samym sobą"). Dla sygnałów ciągłych <math>\langle x(t), x(t) \rangle = \int |x(t)|^2 dt</math>, dla sygnałów dyskretnych <math> \langle x[n], x[n] \rangle = \sum_n |x[n]|^2</math>. |
Fizycznie musimy wziąć pod uwagę wspomniane wcześniej stałą kalibracji i częstość próbkowania: | Fizycznie musimy wziąć pod uwagę wspomniane wcześniej stałą kalibracji i częstość próbkowania: | ||
Aktualna wersja na dzień 17:24, 16 lis 2024
Spis treści
⬆ Próbkowanie sygnałów analogowych
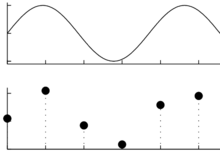
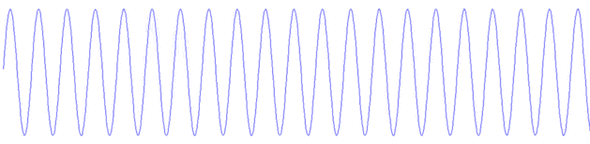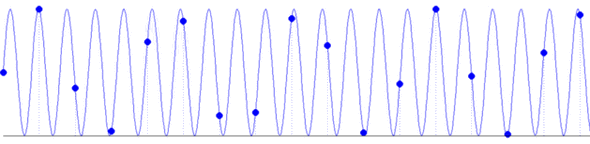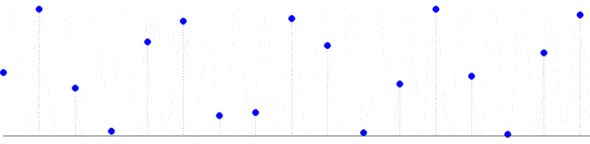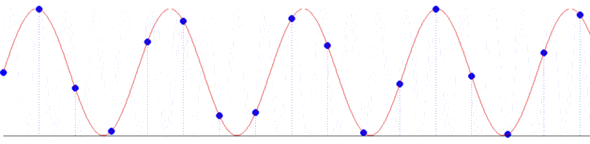
Sygnały zapisujemy, przetwarzamy i analizujemy w postaci ciągów liczb. Przejście od sygnału ciągłego do cyfrowego odbywa się przez proces próbkowania, czyli zapisywania kolejnych amplitud sygnału w ustalonych, stałych odstępach czasu, omawiany wcześniej na TIiK.
102, 195, 80, 16, 147, 178
Żeby odtworzyć fizyczne własności sygnału, czyli narysować zapisane wartości próbek w odpowiedniej skali, musimy znać częstość próbkowania i stałą kalibracji.
Wyrażana w hercach (Hz) częstość próbkowania (ang. sampling frequency, [math]f_s[/math]) to liczba próbek na sekundę. Jest ona odwrotnością odstępu w czasie między kolejnymi próbkami ([math]\Delta t[/math]):
[math]f_s = \dfrac{1}{\Delta t}[/math]
Stała kalibracji to współczynnik, przez który mnożymy zapisane liczby, żeby otrzymać wartości w jednostkach fizycznych, na przykład mikrowoltach.
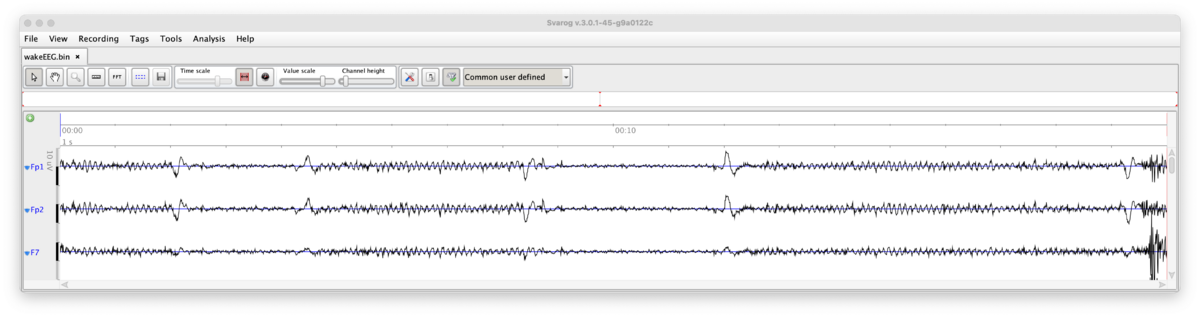
Oczywiście musimy też wiedzieć, w jakim formacie zapisano na dysku liczby (formaty omawialiśmy na wykładzie o binarnych reprezentacjach liczb), oraz, w przypadku sygnałów wielozmiennych o jednolitym próbkowaniu, znać liczbę kanałów. Taka dodatkowa informacja (metainformacja) jest konieczna do poprawnego wyświetlenia danych z pliku, w którym zapisano dane wielokanałowe, jak np. kilka odprowadzeń EEG lub dane kilku spółek giełdowych, próbkowane i zapisywane w jednakowych odstępach czasu.
| RozwińInformacje o częstości próbkowania, stałej kalibracji, liczbie i nazwach kanałów itp. to metainformacja, klucz do poprawnego odczytu i intepretacji zapisanych liczb. |
Aliasing i częstość Nyquista
W procesie próbkowania kluczową rolę odgrywa twierdzenie o próbkowaniu (inaczej twierdzenie Nyquista-Shannona, czasem w skrócie twierdzenie Nyquista). Mówi ono, że sygnał ciągły możemy odtworzyć za zapisanych próbek, jeśli częstość próbkowania [math]f_s[/math] była wyższa niż dwukrotność najwyższej z występujących w sygnale częstości [math]f_{max}[/math], nazywana częstością Nyquista [math]f_N[/math]:
[math] f_s = \dfrac{1}{\Delta t} \gt 2* f_{max} = f_N[/math]
Jeśli częstość próbkowania nie była wystarczająco wysoka, nie tylko stracimy informację o zmianach amplitudy sygnału "pomiędzy próbkami", ale dojdzie też do zafałszowania sygnału w niższych częstościach, które z pozoru nie powinny być zaburzone. Efekt ten jest bliżej omówiony w rozdziale Aliasing.
Sygnał dyskretny jako wektor
Skoro sygnał to po prostu ciąg liczb, możemy go potraktować jak wektor. Na płaszczyźnie wektor to para współrzędnych (x, y), w przestrzeni trójwymiarowej trójka liczby (x, y, z), które wyobrażamy sobie jako strzałkę wiodącą od punktu (0, 0, 0) do (x, y, z). Sygnał składający się z pięciu punktów będzie wektorem w przestrzeni pięciowymiarowej, więc intuicja "strzałki" dla większości z nas przestaje być użyteczna. Pomimo tego, możemy wciąż korzystać z użytecznych pojęć z dziedziny algebry wektorów, jak ortogonalność czy iloczyn skalarny.
Iloczyn skalarny
Iloczyn skalarny przyjmiemy jako miarę podobieństwa dwóch sygnałów. Obliczać go będziemy tak samo jak dla wektorów — przypomnijmy: niech [math]\mathbf{x} = [x_1, x_2, x_3][/math], i [math]\mathbf{y} = [y_1, y_2, y_3][/math]; iloczyn skalarny tych wektorów oznaczamy [math]\mathbf x \cdot \mathbf y[/math] (zarówno wytłuszczenie symboli wektorów, jak i symbol mnożenia/ilocznu skalarnego "[math]\cdot[/math]", będziemy dalej pomijać):
[math]\displaystyle \mathbf a \cdot \mathbf b = \sum_{i=1}^3 x_i y_i = x_1 y_1 + x_2 y_2 + x_3 y_3[/math]
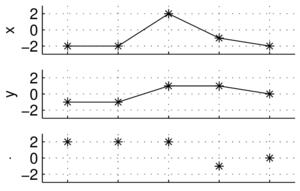
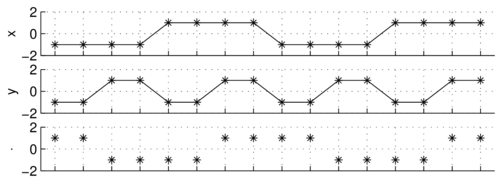
A jak to będzie wyglądać dla sygnałów złożonych z więcej niż trzech punktów? Weźmy
[math]x=[-2, -2, 2, -1, -2][/math]
[math]y=[-1, -1, 1, 1, 0][/math]
Zamiast strzałek w pięciowymiarowej przestrzeni, łatwiej wizualizować na wykresach wartości kolejnych próbek:
[math]x\cdot y = [-2, -2, 2, -1, -2] \cdot [-1, -1, 1, 1, 0] = 2+2+2-1+0 = 5[/math]
Ortogonalność
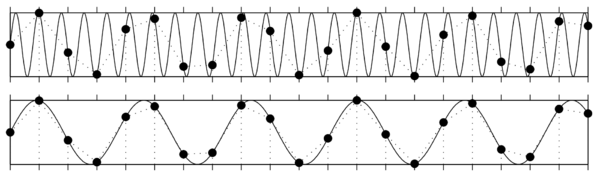
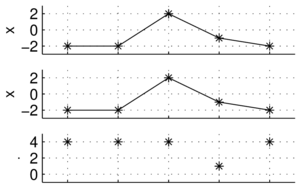
Kolejnym użytecznym pojęciem, które możemy zaczerpnąć bezpośrednio z algebry wektorów, jest ortogonalność. Dwa wektory (sygnały) są do siebie ortogonalne, jeśli ich iloczyn skalarny wynosi zero, jak poniżej:
W przypadku sygnału złożonego z 16 punktów, możemy ten fakt sprawdzić obliczając iloczyn skalarny punkt po punkcie, albo też zauważając prawidłowości występujące w każdym okresie górnego sygnału. W przypadku dłuższych i bardziej złożonych sygnałów może to już nie być takie oczywiste, jak np. ortogonalność wszystkich sinusów na poniższym rysunku, których częstości są całkowitymi wielokrotnościami częstości podstawowej:
| RozwińZbiór ortogonalnych sinusów |
Energia sygnału
Matematycznie energia sygnału [math]x[/math] to [math]\langle x,x \rangle[/math] (czyli [math]x\cdot x[/math], iloczyn skalarny sygnału "z samym sobą"). Dla sygnałów ciągłych [math]\langle x(t), x(t) \rangle = \int |x(t)|^2 dt[/math], dla sygnałów dyskretnych [math] \langle x[n], x[n] \rangle = \sum_n |x[n]|^2[/math]. Fizycznie musimy wziąć pod uwagę wspomniane wcześniej stałą kalibracji i częstość próbkowania:
- Jeśli sygnałem będzie prąd elektryczny o natężeniu [math]i(t)[/math] mierzonym w amperach, płynący w obwodzie o oporności [math]R[/math] omów, to wytracana przez niego energia wyniesie [math]E_i = R \int |i(t)|^2 dt[/math] dżuli.
- W przypadku sygnału dyskretnego [math]x[t][/math], całkę [math]\int x(t) dt [/math] zastępujemy sumą pól kolejnych prostokątów o wysokości [math]x[n][/math] i szerokości równej odstępowi między kolejnymi punktami [math]\Delta t = \frac{1}{f_s}[/math]
- [math]E_{x[n]} = \Delta t \sum_n |x(n)|^2 = \frac{1}{f_s} \sum_n |x(n)|^2 [/math]
Liczby zespolone
Przypomnijmy w skrócie: [math]i^2=-1[/math]. Liczbę zespoloną [math]z[/math] możemy zapisać w postaci algebraicznej jako
- [math]z=a+bi,[/math]
gdzie [math]a[/math] to część rzeczywista, [math]b[/math] — część urojona.
Sprzężenie zespolone liczby [math]z[/math] oznaczamy [math]\overline{z}[/math]:
- [math]\overline{z} = a - bi[/math]
a jej moduł to [math]|z| = \sqrt{a^2 + b^2}[/math] (inaczej [math]|z| = z \cdot \overline{z}[/math]).
Postać trygonometryczna:
- [math]z = a + bi = |z| \cdot \dfrac{a}{|z|} + |z| \cdot \dfrac{b}{|z|}i = |z| \cdot (\cos \phi + i\sin \phi).[/math]
Wykorzystując wzór Eulera[1]
- [math]e^{i\phi} = \cos(\phi) + i\sin(\phi)[/math]
możemy liczbę zespoloną zapisać jako
- [math]z = |z|e^{i\phi}[/math]
Szereg Fouriera
Sygnał okresowy (o okresie [math]T[/math]) można przedstawić w postaci szeregu Fouriera:
gdzie
| RozwińDowód powyższego wzoru: |
Każdą funkcję okresową możemy przedstawić w postaci sumy sinusów i kosinusów z odpowiednimi wagami — przypomnijmy: [math]e^{i \phi} = \cos(\phi) + i \sin(\phi)[/math].
Wagi [math]c_n[/math] możemy traktować jako względny udział odpowiadających im częstości.
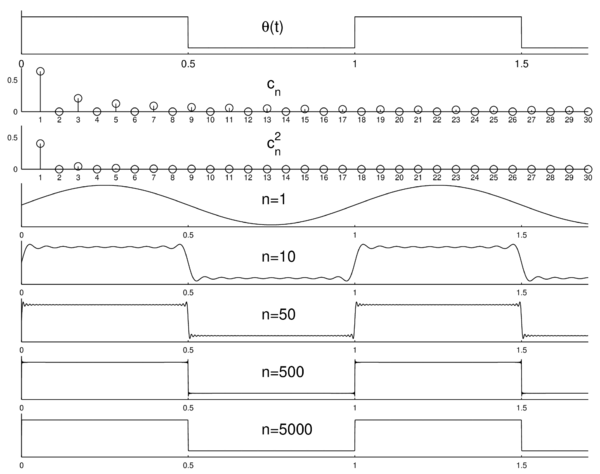
Przykład: szereg Fouriera dla prostokąta
Policzmy postać współczynników Fouriera dla funkcji [math]\Theta(t)[/math], określonej na przedziale [math][0,1][/math] w następujący sposób:
- [math] \Theta(t) = \left\{ \begin{matrix} 1 &, & t \in [0, \frac{1}{2})\\ 0 &, & t \in [ \frac{1}{2}, 1] \end{matrix} \right. [/math]
| Rozwińobliczenia: |
Dostajemy
Od góry, kolejno:
funkcja [math]\Theta[/math] (równanie 3) uzupełniona do funkcji okresowej, pierwszych 30 współczynników szeregu Fouriera,
kwadraty współczynników szeregu Fouriera — dyskretne widmo,
pierwszy wyraz rozwinięcia Fouriera, sumy pierwszych 10, 50, 500 i 5000 wyrazów rozwinięcia 4.
Jak widać, najtrudniejsza do wyrażenia z pomocą funkcji
trygonometrycznych jest nieciągłość funkcji [math]\theta(t)[/math] w punktach [math]\left\{\pm \frac{k}{2}, k \in N \right\}[/math]; niejednorodna
zbieżność szeregów Fouriera w tych rejonach nosi nazwę efektu Gibbsa.
Przekształcenie Fouriera
Przejdźmy do nieskończoności z okresem sygnału: [math]T\rightarrow\infty[/math]. Wtedy odstęp [math]\left(\frac{2\pi}{T}\right)[/math] między częstościami kolejnych elementów sumy szeregu Fouriera
[math]\displaystyle s(t) =\sum_{n=-\infty}^{+\infty} c_n e^{-i\frac{2\pi t}{T} n}, [/math]
dąży do [math]0[/math] i suma przechodzi w całkę
funkcja [math]\hat{s}(f)[/math], zastępująca dyskretny ciąg współczynników szeregu Fouriera
[math]\displaystyle c_{n} = \frac{1}{T}\int_{0}^{T} s(t) e^\frac{2\pi i n t}{T} d t [/math]
to transformata Fouriera sygnału [math]s(t)[/math], czyli wynik działania przekształcenia (transformacji) Fouriera [math]\mathcal{F}[/math].
- ↑ wzorem Eulera bywa również nazywane równanie [math]e^{i\pi}+1=0[/math]
