Aliasing: Różnice pomiędzy wersjami
| Linia 1: | Linia 1: | ||
==[[Analiza_sygnałów_-_lecture|AS/]] Przekształcenie Fouriera sygnałów dyskretnych, aliasing== | ==[[Analiza_sygnałów_-_lecture|AS/]] Przekształcenie Fouriera sygnałów dyskretnych, aliasing== | ||
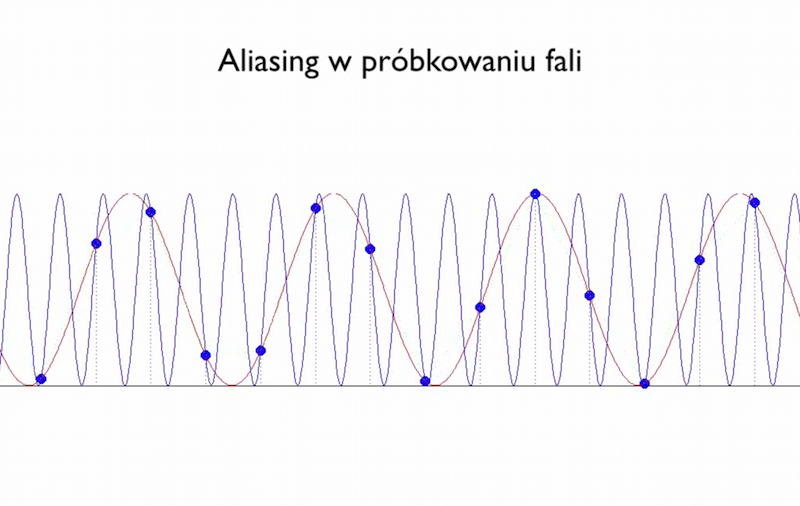
| − | [[Media:aliasing.ogv| | + | [[Media:aliasing.ogv|'''Kliknij na tym napisie aby obejrzeć animację pokazującą efekt aliasingu na sygnale jednowymiarowym''']] |
| + | |||
| + | [[Plik:aliasingklatka.png]] | ||
Przypomnijmy [[Przekształcenie Fouriera#label-eq:21|wzór na odwrotną transformację Fouriera]] sygnału ciągłego | Przypomnijmy [[Przekształcenie Fouriera#label-eq:21|wzór na odwrotną transformację Fouriera]] sygnału ciągłego | ||
Wersja z 08:40, 6 paź 2015
AS/ Przekształcenie Fouriera sygnałów dyskretnych, aliasing
Kliknij na tym napisie aby obejrzeć animację pokazującą efekt aliasingu na sygnale jednowymiarowym
Przypomnijmy wzór na odwrotną transformację Fouriera sygnału ciągłego
[math] s(t)=\int_{-\infty}^{\infty}\hat{s}(f)e^{-i 2\pi t f} d f [/math]
Dyskretne wartości tego sygnału, próbkowane w chwilach [math]n \Delta t[/math], możemy odtworzyć z powyższgo równania dla [math]t = n \Delta t[/math]
[math] \sum_{r=-\infty}^\infty \int_\frac{(2r - 1)}{2\Delta t}^\frac{(2r + 1) }{2\Delta t} \hat{s}(f)e^{-i 2\pi n \Delta t f} d f \;\; \stackrel{f \rightarrow f+\frac{r}{\Delta t}}{=} \;\; [/math] [math] \sum_{r=-\infty}^\infty \int_\frac{-1}{2\Delta t}^\frac{1}{2\Delta t} \hat{s}\left(f + \frac{r}{\Delta t}\right)e^{-i 2\pi n \Delta t (f + \frac{r}{\Delta t})} d f [/math]
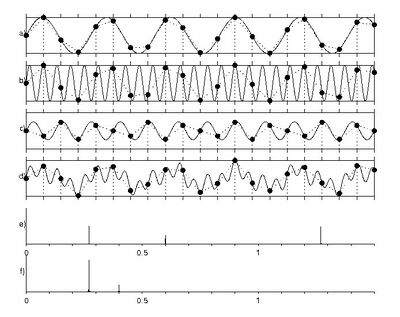
[math] = \int_\frac{-1}{2\Delta t}^\frac{1}{2\Delta t} \sum_{r=-\infty}^\infty \hat{s}\left(f + \frac{r}{\Delta t}\right)e^{-i 2\pi n \Delta t f} d f [/math]Szukając wartości sygnału w dyskretnych chwilach czasu, dostaliśmy w miejsce odwrotnej transformaty Fouriera całkę w ograniczonym zakresie z funkcji będącej (nieskończoną) sumą powtórzeń transformaty Fouriera sygnału ciągłego, przesuwanej o wielokrotności odwrotności [math]\Delta t[/math]. Ilustruje to rysunek %i 1.