WnioskowanieStatystyczne/Test serii

Wnioskowanie_Statystyczne_-_wykład

Test serii Walda-Wolfowitza

Serią nazywamy ciąg jednakowych elementów. W poniższym przykładzie mamy sześć serii (po trzy serie zer i jedynek):

[math]\underline{1}\overline{00}\underline{1}\overline{00}\underline{111} \overline{0}[/math].

Nie jest to oczywiście jedyna kombinacja kolejności pięciu zer i jedynek, dająca w wyniku sześć serii. Ponieważ każda pojedyncza kombinacja jest jednakowo prawdopodobna (jeśli jest wynikiem niezależnych losowań), to prawdopodobieństwo uzyskania danej liczby serii będzie tym większe, im więcej różnych kombinacji będzie dawać w wyniku tę liczbę serii. Sformułujmy więc problem ogólnie:

Mamy [math]N=n_1+n_2[/math] elementów, w tym [math]n_1[/math] zer i [math]n_2[/math] jedynek. Na ile sposobów możemy je rozłożyć, aby uzyskać [math]k[/math] serii?

Na przedstawiony powyżej przykład, zawierający pięć jedynek i pięć zer, możemy patrzeć jak na przypisanie liczbom od jeden do dziesięciu (pozycje w ciągu) zera lub jedynki:

1	0	0	1	0	0	1	1	1	0
1	2	3	4	5	6	7	8	9	10

Inaczej mówiąc, konkretny ciąg [math]N[/math] zer i jedynek wyznaczony jest przez wylosowanie spośród liczb od jednego do [math]N[/math] tych liczb, którym mają być przypisane jedynki (pozostałym będą przypisane zera — lub odwrotnie). Czyli wszystkich możliwych ciągów [math]n_1[/math] zer i [math]n_2[/math] jedynek będzie tyle, na ile sposobów można wylosować [math]n_1[/math] elenentów spośród [math]N[/math]. Policzmy: pozycję (czyli numer, wypisany w dolnym rzędzie powyższej tabeli) pierwszego elementu losujemy spośród [math]N[/math] możliwości, drugiego — spośród [math]N-1[/math] pozostałych możliwości (jedna pozycja jest już zajęta), i tak dalej, aż pozycję ostatniego z [math]n_1[/math] elementów losujemy spośród [math]N-n_1[/math] pozostałych możliwości. Liczba możliwych wyników będzie iloczynem tych wszystkich liczb, czyli wyniesie [math]N\cdot(N-1)\cdot(N-2)\cdot\ \dots\ \cdot (N-n_1) = N!/(N-n_1)![/math] Skoro wszystkie jedynki są jednakowe i nie rozróżniamy wyników różniących się ich kolejnością, to wynik ten musimy podzielić przez liczbę różnych ustawień kolejności elementów (liczbę permutacji) zbioru [math]n_1[/math]-elementowego. Wyniesie ona [math]n_1\cdot(n_1-1)\cdot\ \dots\ \cdot 1[/math], czyli [math]n_1![/math] Ostatecznie jako liczbę różnych ustawień [math]n_1[/math] zer i [math]N-n_1[/math] jedynek dostajemy:

[math] \frac{N!}{(N-n_1)!\ n_1!} = \binom{N}{n_1}. [/math]

Jest to znany z rozdziału o rozkładzie dwumianowym symbol Newtona [math]\binom{N}{n_1}[/math]. Jego własności symetrii zgadzają się z sytuacją, w ktorej "wybierać" możemy albo [math]n_1[/math] zer albo [math]n_2[/math] jedynek:

[math] \binom{N}{n_1}=\binom{n_1+n_2}{n_1}=\frac{(n_1+n_2)!}{n_1! n_2!}=\binom{n_1+n_2}{n_2}=\binom{N}{n_2}. [/math]

Pozostaje policzyć, ile z tych możliwości (przy ustalonych liczbach [math]n_1[/math] jedynek i [math]n_2[/math] zer) wygeneruje ciąg wyników, w którym będzie dokładnie [math]k[/math] serii?

1. Jeśli liczba serii [math]k[/math] jest parzysta, to będziemy mieć tyle samo serii jedynek i zer (po [math]k/2[/math]). Aby rozmieścić [math]n_1[/math] jedynek w [math]k/2[/math] seriach musimy wyznaczyć [math]k/2-1[/math] punktów podziału na serie; w powyższym przykładzie będą to (kropki) 1.1.111. — było 6 serii, więc mamy 2 punkty podziału. Inaczej losujemy spośród [math]n_1-1[/math] możliwych punktów podziału [math]k/2-1[/math] podziałów, jak wynika z liczby serii [math]k[/math]. Daje to [math]\binom{n_1-1}{k/2-1}[/math] możliwości. W miejsca podziału (oznaczone kropkami) wstawiamy serie zer; analogicznie możemy to zrobić na [math]\binom{n_2-1}{k/2-1}[/math] możliwości (w przykładzie: 00.00.0). Liczbę tę należy pomnożyć przez dwa ze względu na możliwość zamiany miejscami zer i jedynek. Prawdopodobieństwo danej liczby serii dostaniemy — zgodnie z klasyczną definicją prawdopodobieństwa — dzieląc liczbę wszystkich tych kombinacji [math]n_1[/math] jedynek i [math]n_2[/math] zer, które generują dokładnie [math]k[/math] serii, przez liczbę wszystkich możliwych kombinacji: [math] P=\frac{ 2\binom{n_1-1}{k/2-1} \binom{n_2-1}{k/2-1}} { \binom{N}{n_1}} \qquad\textrm{dla }\ k\ \textrm{parzystych.} [/math]
2. Jeśli liczba serii [math]k[/math] jest nieparzysta, to którychś serii — zer lub jedynek — będzie dokładnie o jeden więcej.
   1. jeśli więcej jest serii jedynek, mamy [math](k-1)/2[/math] serii zer i [math](k-1)/2+1[/math] serii jedynek. [math]n_1[/math] jedynek dzielimy na [math](k-1)/2+1[/math] serii, czyli wyznaczamy [math](k-1)/2[/math] punktów podziału spośród [math]n_1-1[/math] możliwych — daje to [math]\binom{n_1-1}{(k-1)/2}[/math] możliwości. Z kolei [math]n_2[/math] zer dzielimy na [math](k-1)/2[/math] serii, co daje [math]\binom{n_2-1}{(k-1)/2-1}[/math] możliwości. Iloczyn tych dwóch wielkości określa liczbę możliwości dających [math]k[/math] serii, jeśli więcej jest serii jedynek:
      [math] \binom{n_1-1}{(k-1)/2} \binom{n_2-1}{(k-1)/2-1} [/math]
   2. jeśli więcej jest serii zer, to na drodze analogicznego rozumowania dostajemy
      [math] \binom{n_1-1}{(k-1)/2-1} \binom{n_2-1}{(k-1)/2}. [/math]

Prawdopodobieństwo dla przypadku nieparzystej liczby serii będzie sumą tych dwóch wielkości podzieloną, jak w przypadku parzystego [math]k[/math], przez liczbę wszystkich możliwości:

[math]\begin{matrix} P&\!\!\!\!=&\!\!\!\!\frac{ \binom{n_1-1}{(k-1)/2} \binom{n_2-1}{(k-1)/2-1} + \binom{n_1-1}{(k-1)/2-1} \binom{n_2-1}{(k-1)/2} } {{ \binom{N}{n_1}}} \\ &&\textrm{dla }\ k\ \textrm{ nieparzystych.} \end{matrix}[/math]

Pozostaje jeszcze rozważyć sytuację, w której liczba serii jest nieparzysta, jak w punkcie 2., ale mniej liczne elementy rozłożone są wyłącznie w serie jednoelementowe, na przykład 001010010100, czyli liczba serii wynosi [math]2n+1[/math], gdzie [math]n[/math] jest liczbą mniej licznych elementów (w tym przykładzie jedynek). Wtedy znika jeden ze składników sumy z licznika powyższego równania, gdyż zachodzić może wyłącznie przypadek 2.1 lub 2.2.

Ostatecznie dostajemy następujący wzór na prawdopodobieństwo wystąpienia [math]k[/math] serii w próbie, w której drogą niezależnych losowań wylosowano [math]n_1[/math] zer i [math]n_2[/math] jedynek:

[math] P(k\mid n_1, n_2)=\begin{cases} \frac{ 2\binom{n_1-1}{k/2-1} \binom{n_2-1}{k/2-1}} { \binom{N}{n_1}} \quad \textrm{dla }\ k\ \textrm{ parzystych} \\ \frac{ \binom{n_1-1}{(k-1)/2} \binom{n_2-1}{(k-1)/2-1} + \binom{n_1-1}{(k-1)/2-1} \binom{n_2-1}{(k-1)/2} } {{ \binom{N}{n_1}}} \\ \quad\qquad\qquad\qquad\qquad\qquad \textrm{dla }\ k\ \textrm{ nieparzystych} \\ \frac{ \binom{n_\textrm{max}-1}{(k-1)/2} } {{ \binom{N}{(k-1)/2}}} \ \quad\qquad\qquad\textrm{dla }\ k\ \textrm{ nieparzystych \ i \ } n_\textrm{min}=\frac{k-1}{2}, \end{cases} [/math]

gdzie [math]n_\textrm{min}=\min(n_1, n_2)[/math] i [math]n_\textrm{max}=\max(n_1, n_2)[/math].

Wzór ten określa rozkład statystyki, będącej liczbą serii w próbie złożonej z dowolnych dwóch rodzajów elementów (oznaczanych powyżej jako 0 i 1). Dzięki niemu możemy wreszcie skonstruować kompletny test hipotezy mówiącej, że dany ciąg jest wynikiem niezależnych losowań. Przypomnijmy dane z przykładu o nieuczciwym ankieterze:

1101101000101001011101101111010110010101001010100011101

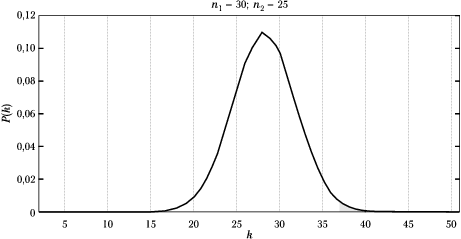
W ciągu tym występuje 25 zer i 30 jedynek, układających się w 37 serii. Na podstawie wzoru (5) możemy obliczyć rozkład prawdopodobieństwa wylosowania ciągu 25 zer i 30 jedynek, w którym będzie [math]k[/math] serii. Możliwe wartości [math]k[/math] będą w tym przypadku zawierać się między 2 (jedna seria zer i jedna jedynek) a 51 (ponieważ mniej jest zer, największa liczba serii odpowiada przypadkowi, w którym wszystkie zera układają się w serie jednoelementowe). Rozkład prawdopodobieństwa dla tego przypadku przedstawia rysunek %i 1.

Rozkład prawdopodobieństw [math]P(k)[/math] liczby serii [math]k[/math] w niezależnym losowaniu 30 zer i 25 jedynek.

Załączony program oblicza według wzoru (5) rozkład prawdpodobieństwa oraz poziom istotności dla hipotezy mówiącej, że wpisany ciąg jest wynikiem niezależnych losowań. Pozwala on na "zabawę w oszukiwanie": możemy próbować wpisać taki ciąg dwóch symboli, który przejdzie test na niezależność losowań. Okazuje się, że najczęściej wpisujemy ciągi, w których występuje za dużo serii, czyli wpisujemy za krótkie serie jednakowych elementów.

Zastosowania testów opartych na tej statystyce nie ograniczają się do analizy ciągów zer i jedynek (lub innych dwóch elementów). Poniżej przedstawiamy jeszcze dwa testy korzystające ze statystyki (5).

Testowanie, czy próba jest wynikiem niezależnych losowań

Podobny problem — pytanie, czy elementy próby są wynikiem niezależnych losowań — występuje np. przy testowaniu generatorów liczb losowych (będących kluczowym elementem metod opisywanych w pierwszej części książki). Jednak w tej sytuacji mamy do czynienia z ciągiem dowolnych liczb, a nie dwóch symboli.

Pomysł jest prosty: ciąg wyników wyrażających się dowolnymi liczbami możemy zamienić na ciąg zer i jedynek, wybierając próg [math]M[/math] i przypisując wynikom większym od [math]M[/math] jedynkę, a mniejszym — zero. Jeśli chcemy mieć tyle samo zer i jedynek, jako [math]M[/math] możemy wziąć medianę próby. Do takiej serii możemy już z powodzeniem stosować opisany w poprzednim rozdziale test oparty na statystyce (5) — oczywiście zachowując kolejność elementów w próbie.

Test zgodności rozkładów w dwóch populacjach

Mamy dwie próby. Hipoteza zerowa mówi, że zostały wylosowane z tego samego rozkładu. Ciąg zer i jedynek tworzymy w następujący sposób:

Elementy obu prób ustawiamy w jeden ciąg w kolejności od najmniejszej do największej. Elementom pierwszej próby przypisujemy jedynki, a drugiej — zera.

Jeśli obie próby losowano z tej samej populacji, to ilość serii w tak określonym ciągu podlega statystyce (5), czyli ponownie możemy stosować test Walda-Wolfowitza.

---

<references>