|
|
| (Nie pokazano 5 wersji utworzonych przez jednego użytkownika) |
| Linia 1: |
Linia 1: |
| | | | |
| − | ==Rozkład równomierny==
| + | [[Wnioskowanie_Statystyczne_-_wykład]] |
| | | | |
| − | ... zwany też jednostajnym, prostokątnym lub płaskim, przyjmuje jednakowe wartości dla wszystkich liczb z jakiegoś odcinka (na przykład między zero a jeden), a poza tym odcinkiem ma wartość zero:
| |
| | | | |
| − | <math>\begin{matrix}
| + | ==Rozkłady prawdopodobieństwa== |
| − | p(x) = 1 & \textrm{ dla } & 0\leq x\leq 1
| + | Rozkład prawdpopodobieństwa — zgodnie z nazwą — będzie funkcją określającą, |
| − | \\
| + | jak prawdopodobieństwo rozkłada się pomiędzy możliwe wyniki danego |
| − | p(x) = 0 & \textrm{ dla } & x>1\ \textrm{ lub }\ x<0.
| + | doświadczenia. Mieliśmy już z nim do czynienia w pierwszej części książki, |
| − | \end{matrix}</math>
| + | <xr id="fig:boot+mc_kosz">rysunek %i</xr> przypomina niektóre z tych przypadków. |
| | | | |
| − | [[Plik:Rozklad_plaski.png|300px|thumb|left|<figure id="fig:rozw2"></figure>Rozkład równomierny określony na odcinku od zera do jedynki. | + | [[Plik:Boot+mc_kosz.png|300px|thumb|left|<figure id="fig:boot+mc_kosz"></figure>(a) rozkład liczby jedynek uzyskany z 10 tysięcy repróbkowań ze |
| − | ]] | + | zwracaniem (bootstrap) próby 18 jedynek i 82 zer; |
| | + | (b) liczba trafień na 10 rzutów do kosza, przy średnim prawdopodobieństwie |
| | + | trafienia 0,6 ]] |
| | | | |
| − | Wartość oczekiwana
| + | Nie są to prawdopodobieństwa, gdyż nie spełniają [[WnioskowanieStatystyczne/Prawdopodobienstwo#label-eq:45|aksjomatu]] <math>(0\leq P(A)\leq 1)</math>, który wraz z [[WnioskowanieStatystyczne/Prawdopodobienstwo#label-eq:43|aksjomatem]] <math>(P(\Omega)=1)</math> możemy spełnić dzieląc liczbę wystąpień każdego przypadku przez całkowitą liczbę eksperymentów — |
| | + | wtedy suma wszystkich prawdopodobieństw (czyli <math>P(\Omega)</math>) |
| | + | wyniesie 1. Przykład tak znormalizowanego dyskretnego rozkładu |
| | + | prawdopodobieństwa przedstawia rysunek <xr id="fig:dysk_i_plask">rysunek %i(a)</xr>. |
| | | | |
| − | <math> | + | Pozostaje jeszcze problem formalny: występujące w klasycznej teorii |
| − | \mu =E(x)=\int\limits_0^1 x dx=\left[\frac{x^{2}}{2}\right]_0^1=\frac{1}{2}.
| + | funkcje nie są określone na zdarzeniach, tylko na liczbach. Przejście |
| − | </math> | + | od zdarzeń do odpowiadających im liczb wymaga pojęcia ''zmiennej |
| | + | losowej'' – odwzorowania <math>X(.)</math> z przestrzeni zdarzeń do |
| | + | przestrzeni liczb rzeczywistych. Na przykład w doświadczeniu |
| | + | polegającym na rzucaniu kostką zmienna losowa przypisze liczbę 4 |
| | + | przypadkowi, w którym na górnej ściance rzuconej kostki widać cztery |
| | + | kropki. |
| | | | |
| − | Wariancja
| + | Liczby (czyli zmienne losowe) są już pełnoprawnymi argumentami |
| | + | funkcji, ale z definicją rozkładu prawdopodobieństwa będzie jeszcze |
| | + | trochę kłopotu, jeśli wyniki eksperymentu będą pochodzić z ciągłych |
| | + | przedziałów zmiennej losowej, a nie, jak w przykładach z rysunku <xr id="fig:boot+mc_kosz">rysunek %i</xr>, ze zbioru dyskretnego. |
| | | | |
| − | <math>
| + | ==Rozkłady ciągłe — gęstość prawdopodobieństwa== |
| − | \sigma ^{2}=E((x-\mu )^{2})= \int\limits_0^1 \left(x-\frac 1 2 \right)^2 dx =
| |
| − | \int\limits_0^1\left(x^2 - x +\frac 14\right) dx = \left[\frac{x^3}3 - \frac{x^2}2 +\frac x 4
| |
| − | \right]^1_0 = \frac 1 {12}.
| |
| − | </math>
| |
| | | | |
| − | Oczywiście rozkład jednostajny może być określony na dowolnym odcinku <math>(a, b)</math> — wystarczy przeskalować opisaną powyżej kanoniczną postać:
| + | [[Plik:Rozklad_dyskretny_i_plaski.png|300px|thumb|left|<figure |
| | + | id="fig:dysk_i_plask"></figure>(a) dyskretny rozkład prawdopodobieństw |
| | + | wyników rzutu kostką; (b) ciągły rozkład prawdopodobieństwa dla liczb |
| | + | rzeczywistych z przedziału od zera do jednego. ]] |
| | | | |
| − | <math>\begin{matrix}
| + | Z rozkładem ciągłym mieliśmy do czynienia, gdy używaliśmy generatora |
| − | p(x) = \frac{1}{b-a} & \textrm{ dla } & a\leq x\leq b
| + | liczb losowych — losował on z równym prawdopodobieństwem liczby |
| − | \\
| + | rzeczywiste z przedziału od zera do jednego. Funkcja przypisująca |
| − | p(x) = 0 & \textrm{ dla } & x<a\ \textrm{ lub }\ x>b.
| + | równe prawdopodobieństwa liczbom od zera do jednego powinna wyglądać |
| − | \end{matrix}</math>
| + | jak na <xr id="fig:dysk_i_plask">rysunku %i(b)</xr>. A jednak coś się |
| | + | tu nie zgadza... |
| | | | |
| − | Proste modyfikacje przytoczonych powyżej całek wykażą, że jego wartość oczekiwana wynosi
| + | Zacznijmy od rozkładu dyskretnego, czyli <xr |
| | + | id="fig:dysk_i_plask">wykresu %i(a)</xr>. Prawdopodobieństwo dla |
| | + | zmiennej losowej (teraz nie jest to już formalnie zdarzenie) |
| | + | wynoszącej na przykład 2 odczytujemy jako wynoszące 0,167. Czyli |
| | + | mniejsze od 1 i większe od zera. Suma prawdopodobieństw dla wszystkich |
| | + | możliwych wartości zmiennej losowej wyniesie 1 — wszystko zgadza się |
| | + | z [[WnioskowanieStatystyczne/Prawdopodobienstwo#Częstościowa definicja prawdopodobieństwa|aksjomatami definicji prawdopodobieństwa]]. |
| | | | |
| − | <math>\frac{a+b}{2},</math> | + | Teraz spróbujmy z wykresu po prawej stronie odczytać wartość |
| | + | prawdopodobieństwa wylosowania jakiejś liczby spomiędzy 0 i 1. Jeden? |
| | + | To oznacza pewność — niemożliwe. Na osi <math>y</math> powinna |
| | + | występować jakaś znacznie mniejsza wartość... Ale jaka? |
| | | | |
| − | a wariancja
| + | Zastanówmy się: niezależnie od tego, jak małą (niezerową i nieujemną) |
| | + | wartość przyjmiemy dla prawdopodobieństwa wylosowania dowolnej liczby |
| | + | z tego przedziału, to gdy zaczniemy je sumować dla wszystkich |
| | + | możliwych wyników, których na odcinku <math>(0, 1)</math> jest wszak |
| | + | nieskończenie wiele, zawsze dostaniemy więcej niż jeden. Najwyraźniej |
| | + | tak się nie da. |
| | | | |
| − | <math>\frac{(b-a)^2}{12}</math>. | + | Widać już, że sumę będziemy musieli zastąpić całką — jest to właśnie |
| | + | graniczny przypadek sumy. W tym układzie aksjomat |
| | + | <math>P(\Omega)=1</math>, który dla przypadku dyskretnego wyrażał się |
| | + | sumą |
| | | | |
| | + | <math> |
| | + | \sum_i P(X=x_i) = 1, |
| | + | </math> |
| | | | |
| − | ==Rozkład dwumianowy==
| + | teraz będzie wyrażał się całką |
| | | | |
| − | Powtarzamy <math>n</math> razy doświadczenie o dwóch możliwych
| + | <math> |
| − | wynikach <math>A</math> i <math>\overline{A}</math> oraz
| + | \int p(x) dx = 1, |
| − | prawdopodobieństwach odpowiednio <math>p</math> i <math>q</math>, przy
| |
| − | czym <math>p+q=1</math>. Wynik <math>A</math> nazywamy sukcesem i
| |
| − | pytamy, jakie jest prawdopodobieństwo <math>k</math> sukcesów?
| |
| − | | |
| − | Liczba <math>k</math>-elementowych podciągów ciągu
| |
| − | <math>n</math>-elementowego wynosi <math>\frac{n!}{(n-k)!}</math>,
| |
| − | czyli <math>n(n-1)(n-2)...(n-k+1)</math>; na pierwszym miejscu każdego
| |
| − | z ciągów możemy ustawić każdy z <math>n</math> elementów, po jego
| |
| − | ustaleniu na drugim miejscu każdy z <math>n-1</math> elementów itd.
| |
| − | Jeśli ponadto nie rozróżniamy podciągów o różnej kolejności elementów,
| |
| − | to liczbę tę podzielić należy przez ilość permutacji (przestawień)
| |
| − | zbioru <math>k</math>-elementowego, czyli <math>k!</math>. W rezultacie
| |
| − | dostajemy <ref> Symbol <math>\binom{n}{k}</math> występuje również we
| |
| − | wzorze na wspólczynniki <math>n</math>-tej potęgi sumy: <math>
| |
| − | (a+b)^{n}=\sum_{k=0}^n \binom{n}{k}a^{k}b^{n-k} </math>
| |
| − | </ref>
| |
| − | | |
| − | <equation id=eq:68">
| |
| − | <math>
| |
| − | \frac{n!}{k!(n-k)!}=\binom{n}{k}.
| |
| − | </math>
| |
| − | </equation>
| |
| − | | |
| − | Niech <math>P_{n}(k)</math> oznacza prawdopodobieństwo wystąpienia
| |
| − | <math>k</math> razy zdarzenia o prawdopodobieństwie <math>p</math> w
| |
| − | serii <math>n</math> powtórzeń. Prawdopodobieństwo jednej serii
| |
| − | <math>k</math> zdarzeń <math>A</math> i <math>(n-k)</math> zdarzeń
| |
| − | <math>\overline{A}</math> wynosi <math>p^k q^{(n-k)}</math>. Zgodnie
| |
| − | z powyższymi rozważaniami, takich serii, które różnią się kolejnością
| |
| − | wystąpienia zdarzeń <math>p</math> i <math>q</math>, będzie
| |
| − | <math>\binom n k</math>. Ostatecznie rozkład dwumianowy możemy opisać
| |
| − | następującym wzorem:
| |
| − | | |
| − | | |
| − | <math> | |
| − | P_{n}(k)=\binom{n}{k}p^{k}q^{n-k}=\frac{n!}{k!(n-k)!}p^{k}(1-p)^{n-k}.
| |
| − | </math>
| |
| − | | |
| − | Rysunek <xr id="fig:rozw2"> %i</xr> przedstawia rozkłady dwumianowe
| |
| − | dla różnych wartości <math>p</math> i <math>n</math>. Wartość
| |
| − | oczekiwana <math>\mu</math> i wariancja <math>\sigma^2</math> rozkładu
| |
| − | dwumianowego wyrażają się następującymi wzorami:
| |
| − | | |
| − | <math>
| |
| − | \mu=np, \qquad \sigma^2=npq.
| |
| − | </math>
| |
| − | | |
| − | ===Dowód===
| |
| − | | |
| − | Bezpośrednie rachunki są w tym przypadku żmudne, więc dla znalezienia
| |
| − | wartości oczekiwanej i wariancji rozkładu dwumianowego posłużymy się
| |
| − | zmienną losową <math>x_{i}</math>, opisującą wynik pojedynczego
| |
| − | doświadczenia. Przyjmuje ona wartość 1, jeśli zaszło zdarzenie
| |
| − | <math>A</math> (sukces) i 0 w przypadku porażki. Rozkład liczby
| |
| − | sukcesów w serii <math>n</math> powtórzeń opisuje zmienna będąca ich
| |
| − | sumą <math>X=\sum\limits_{i=1}^n x_{i}</math>.
| |
| − | | |
| − | Wartość oczekiwana zmiennej <math>x_i</math>, czyli wyniku ''pojedynczego''
| |
| − | doświadczenia, wynosi
| |
| − | | |
| − | <math>
| |
| − | E(x_i)=\sum\limits_i x_i P(X=x_i) = 1\cdot p + 0\cdot q = p.
| |
| − | </math>
| |
| − | | |
| − | Wartość oczekiwana sumy <math>n</math> zmiennych <math>x_i</math>,
| |
| − | dającej wartość zmiennej opisywanej rozkładem dwumianowym, będzie (z
| |
| − | [[STAT:Momenty#label-eq:61|liniowości wartości oczekiwanej]]) sumą
| |
| − | wartości oczekiwanych — stąd wartość oczekiwana rozkładu
| |
| − | dwumianowego wyniesie <math>n p</math>. Z kolei wariancja
| |
| − | <math>x_i</math> wynosi
| |
| − | | |
| − | <math>
| |
| − | \sigma^2(x_i)=E((x_{i}-\mu)^{2})=\sum\limits_i (x_i-p)^2P(X=x_i)= (1-p)^{2}p+(0-p)^{2}q =q^{2}p+p^{2}q=pq(p+q)=pq.
| |
| − | </math>
| |
| − | | |
| − | Wariancja rozkładu dwumianowego będzie równa wariancji sumy <math>n</math> zmiennych <math>x_i</math>. Ponieważ zmienne te są niezależne,
| |
| − | | |
| − | <math>
| |
| − | \sigma^2\left(\sum_{i=1}^{n}x_i\right) = n\sigma^2(x_i) = npq.
| |
| | </math> | | </math> |
| | | | |
| | + | gdzie prawdopodobieństwo <math>P</math> zastąpiła, z przyczyn, które |
| | + | staną się jasne za chwilę, gęstość prawdopodobieństwa <math>p</math>. |
| | + | Łatwo sprawdzić, że całka rozkładu z <xr |
| | + | id="fig:dysk_i_plask">rys. %i</xr> spełnia ten warunek. Jednak |
| | + | pozostaje problem odczytywania wartości prawdopodobieństwa dla |
| | + | konkretnej wartości zmiennej losowej. |
| | | | |
| | + | Przypomnijmy sobie, że [[WnioskowanieStatystyczne/Bootstrap|symulując rzuty monetą]] korzystaliśmy z faktu, że prawdopodobieństwo wylosowania liczby |
| | + | mniejszej niż <math>\frac1 2</math> wynosi 0,5. Zdefiniujmy więc |
| | + | ''dystrybuantę'' prawdopodobieństwa zmiennej losowej <math>X</math> |
| | + | jako prawdopodobieństwo wystąpienia któregokolwiek ze zdarzeń, dla |
| | + | których zmienna losowa przyjmuje wartości mniejsze od <math>x</math>: |
| | | | |
| − | [[Plik:Rozklad_dwumian.png|300px|thumb|left|<figure id="fig:rozw2">
| + | <equation id="eq:59"> |
| − | </figure> Dwumianowe rozkłady prawdopodobieństwa dla <math>p=\frac 1
| |
| − | 6</math>, <math>\frac{1}{2}=\ i\ = 0.8</math> oraz <math>n=5=\ i\ =
| |
| − | 20</math>]]
| |
| − | | |
| − | === Przykład:rozkład dwumianowy===
| |
| − | | |
| − | Obliczmy rozkład prawdopodobieństwa wyrzucenia <math>k</math> szóstek
| |
| − | w pięciu rzutach kostką (symulowany w [[STAT:Z_komputerem|rozdziale o
| |
| − | metodzie Monte Carlo]]): <math>p=\nicefrac{1}{6}</math>, <math>q=\nicefrac{5}{6}</math>,
| |
| − | <math>\binom{5}{0}=1</math>, <math>\binom{5}{1}=5</math> i tak dalej.
| |
| − |
| |
| − | {|class=wikitable
| |
| − | |-
| |
| − | |<math>k=</math>
| |
| − | |0
| |
| − | |1
| |
| − | |2
| |
| − | |3
| |
| − | |4
| |
| − | |5
| |
| − | |-
| |
| − | |<math>P_5(k)\approx</math>
| |
| − | | 0,4019
| |
| − | | 0,4019
| |
| − | | 0,1608
| |
| − | | 0,0322
| |
| − | | 0,0032
| |
| − | | 0,0001
| |
| − | |}
| |
| − | | |
| − | Wartości te przedstawione są na wykresie w lewym górnym rogu rysunku
| |
| − | <xr id="fig:rozw2"> %i</xr>. Prawdopodobieństwo wyrzucenia przynajmniej
| |
| − | dwóch (czyli od dwóch do pięciu) szóstek wynosi
| |
| − | <equation id="eq:70">
| |
| − | <math>0,1608+0,0322+0,0032+0,0001\approx 0,1962</math>.
| |
| − | </equation>
| |
| − | | |
| − | Z kolei rozkład liczby sukcesów w stu takich grach, przybliżany
| |
| − | numerycznie na [[STAT:Z_komputerem#label-fig:13|rysunku]], będzie odpowiadał <math>P_{100}(k)</math> dla <math>p=0,1962</math>.
| |
| − | Suma tego rozkładu dla <math>k>20</math> wynosi <math>0,4034</math>.
| |
| − | | |
| − | === Przykład: trzy dziewczynki===
| |
| − | | |
| − | Obliczmy prawdopodobieństwo, że wśród czworga dzieci będą co najmniej
| |
| − | trzy dziewczynki — zakładając, że prawdopodobieństwa urodzenia dziecka
| |
| − | każdej płci są równe.
| |
| − | | |
| − | "Co najmniej trzy dziewczynki" można zasymulować jako cztery lub trzy
| |
| − | "sukcesy" w czterech "losowaniach płci" o prawdopodobieństwie sukcesu <math>\frac{1}{2}</math>, czyli
| |
| − | | |
| − | <center><math> P_4(4)+P_4(3)=\binom{4}{4}\left(\frac 12\right)^4 +
| |
| − | \binom{4}{3}\left(\frac 12\right)^4 = (1+4)\left(\frac 12\right)^4 =
| |
| − | \frac{5}{16}= 0,3125, </math></center>
| |
| − | | |
| − | zgodnie z wynikiem symulacji z [[zadania]].
| |
| − | | |
| − | ===Przykład:===
| |
| − | | |
| − | W rzutach do kosza uzyskiwaliśmy średnio 6 trafień na 10 rzutów. Po
| |
| − | zmianie techniki w pierwszych 10 rzutach uzyskaliśmy 9 trafień. Czy
| |
| − | należy wnioskować, że nowa technika rzutów poprawia średnią trafień?
| |
| − | | |
| − | Jeśli zmiana techniki nie wpłynęła na skuteczność, to prawdopodobieństwo
| |
| − | uzyskania 9 lub więcej trafień na 10 rzutów odpowiada 9 lub 10 sukcesom w 10
| |
| − | losowaniach o prawdopodobieństwie 0,6, czyli:
| |
| − | | |
| − | <center><math>\begin{matrix}
| |
| − | P_{10}(9)+P_{10}(10)=\binom{10}{9}(0,6)^9 0,4+\binom{10}{10}(0,6)^{10} = \\
| |
| − | = (0,6)^9(10\cdot0,4+0,6)
| |
| − | \approx
| |
| − | 0,0101\cdot 4,6=0,046.
| |
| − | \end{matrix}</math></center>
| |
| − | | |
| − | Czyli mniej niż 5% — zgodnie z wynikiem [[symulacji]].
| |
| − | | |
| − | | |
| − | ==Rozkład Poissona==
| |
| − | | |
| − | W granicy dużej liczby <math>n</math> zdarzeń o niskim
| |
| − | prawdopodobieństwie <math>p</math>, tj. <math>n\rightarrow \infty ,</math> <math>np=\lambda =const., </math> otrzymujemy z rozkładu
| |
| − | dwumianowego rozkład Poissona:
| |
| − | | |
| − | <equation id="eq:72"> | |
| | <math> | | <math> |
| − | P_{n}(k)=P_{\lambda}(k)=\frac{\lambda ^{k}}{k!}e^{-\lambda }.
| + | F(x)=P[X \leq x]. |
| − | </math>
| |
| − | </equation>
| |
| − | | |
| − | ===Dowód===
| |
| − | | |
| − | <math>\begin{matrix}
| |
| − | P_{n}(k)&=&\frac{n!}{k!(n-k)!}p^{k}q^{n-k}=
| |
| − | \frac{n!}{k!(n-k)!}
| |
| − | \left(\frac{\lambda }{n}\right)^{k}\frac{(1-\frac{\lambda
| |
| − | }{n})^{n}}{(1-\frac{\lambda }{n})^{k}}=\\
| |
| − | &=&\frac{\lambda ^{k}}{k!}\frac{n(n-1)...(n-k+1)(1-\frac{\lambda }{n})^{n}}{n^{k}(1-\frac{\lambda }{n})^{k}}=
| |
| − | \\
| |
| − | &=&\frac{\lambda ^{k}}{k!}(1-\frac{\lambda }{n})^{n}\frac{(1-\frac{1}{n})
| |
| − | (1-\frac{2}{n})...(1-\frac{k-1}{n})}{(1-\frac{\lambda }{n})^{k}}.
| |
| − | \end{matrix}</math>
| |
| − | | |
| − | Ponieważ <math>\underset{n\rightarrow \infty }{\lim }
| |
| − | \frac{(1-\frac{1}{n})
| |
| − | (1-\frac{2}{n})...(1-\frac{k-1}{n})}{(1-\frac{\lambda }{n})^{k}} =
| |
| − | 1</math>, oraz <math>\underset{n\rightarrow \infty }{\lim
| |
| − | }(1-\frac{\lambda }{n})^{n}=e^{-\lambda}</math>,
| |
| − | | |
| − | dostajemy <xr id="eq:72">(%i)</xr>.
| |
| − | | |
| − | '''Sprawdźmy warunek [[STAT:Prawdopodobieństwo#label-eq:43|<math>P(\Omega)=1</math>]]'''
| |
| − | | |
| − | Przestrzeń wszystkich możliwych zdarzeń wyczerpują tu liczby sukcesów
| |
| − | <math>k</math> od zera do <math>n</math>
| |
| − | <math>(n\rightarrow\infty)</math>, czyli
| |
| − | | |
| − | <equation id="eq:73">
| |
| − | <math>
| |
| − | P(\Omega)=\sum_{k=0}^{\infty} P_{\lambda }(k)=
| |
| − | \sum_{k=0}^{\infty} \frac{\lambda ^{k}}{k!}e^{-\lambda }=
| |
| − | e^{-\lambda }\sum_{k=0}^{\infty} \frac{\lambda ^{k}}{k!}=
| |
| − | e^{-\lambda }e^{\lambda }=1
| |
| − | </math>
| |
| − | </equation>
| |
| − | | |
| − | gdyż
| |
| − | | |
| − | <equation id="eq:74">
| |
| − | <math>
| |
| − | \sum_{k=0}^{\infty} \frac{\lambda ^{k}}{k!} = e^{\lambda}.
| |
| − | </math>
| |
| − | </equation>
| |
| − | | |
| − | ===Wartość oczekiwana i wariancja===
| |
| − | | |
| − | wynoszą:
| |
| − | <equation id="eq:75">
| |
| − | <math>
| |
| − | \mu(k)=\sigma^2(k)=\lambda.
| |
| | </math> | | </math> |
| | </equation> | | </equation> |
| | | | |
| − | ====Dowód====
| + | Będzie to oczywiście funkcja niemalejąca, dążąca do zera dla małych |
| − | <math> | + | <math>x</math> i do jednego dla dużych. Dla rozkładu z <xr |
| − | E(k)=\underset{k=0}{\overset{\infty }{\sum }}k\frac{\lambda ^{k}}{k!}
| + | id="fig:dysk_i_plask">rysunku %i</xr>(b) dystrybuanta będzie wyglądać |
| − | e^{-\lambda }=\lambda e^{-\lambda }\underset{k=1}{\overset{\infty }{\sum }}
| + | jak na <xr id="fig:plaski">rysunku %i</xr>. |
| − | \frac{\lambda ^{k-1}}{(k-1)!}=\lambda e^{-\lambda }\underset{l=0}{\overset{
| |
| − | \infty }{\sum }}\frac{\lambda ^{l}}{l!}=\lambda e^{-\lambda } e^{\lambda }=\lambda,
| |
| − | </math> | |
| − | | |
| − | <math>\begin{matrix} | |
| − | \sigma ^{2}(k)&
| |
| − | {=}&
| |
| − | E(k^{2})-\{E(k)\}^{2}=\ \left(\underset{k=0}{\overset{\infty }
| |
| − | {\sum}}k^{2}\frac{\lambda ^{k}}{k!}e^{-\lambda } \right) -\lambda ^{2}=
| |
| − | \\
| |
| − | &=&\lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{k\lambda ^{k-1}}{(k-1)!}-\lambda ^{2}
| |
| − | =\lambda \{e^{-\lambda }\underset{l=0}{\overset{\infty }{\sum }}(l+1)\frac{\lambda ^{l}}{l!}-\lambda \}=
| |
| − | \\
| |
| − | &=&\lambda \{e^{-\lambda }\underset{l=0}{\overset{\infty }{\sum }}l
| |
| − | \frac{\lambda ^{l}}{l!}+e^{-\lambda }\underset{l=0}{\overset{\infty }{\sum }}
| |
| − | \frac{\lambda ^{l}}{l!}-\lambda\} =\end{matrix}</math>
| |
| − | | |
| − | z <xr id="eq:74">(%i)</xr>
| |
| | | | |
| − | <math> | + | [[Plik:Dystryb_plaski.png|300px|thumb|left|<figure |
| − | = \lambda (\lambda +1-\lambda )=\lambda .
| + | id="fig:plaski"></figure>Dystrybuanta ciągłej zmiennej losowej o |
| − | </math>
| + | równym prawdopodobieństwie na przedziale (0, 1).]] |
| | | | |
| − | Jeśli wariancja rozkładu Poissona jest równa jego wartości oczekiwanej (<math>\lambda</math>), to odchylenie standardowe <math>\sigma</math> (czyli pierwiastek z wariancji) wyniesie
| + | Dopiero teraz '''gęstość prawdopodobieństwa''' zmiennej losowej określimy jako |
| | + | pochodną dystrybuanty |
| | | | |
| | + | <equation id="eq:59"> |
| | <math> | | <math> |
| − | \sigma ^{2}(k)=\lambda \Rightarrow \sigma (k)=\sqrt{\lambda }=\sqrt{np}.
| + | p(x)=\frac{d F(x)}{dx}=\frac{P[x\leq X\leq x+dx]}{dx}. |
| − | </math>
| |
| − | | |
| − | Wynik ten przytaczany bywa jako "prawo" określające błąd liczby
| |
| − | zliczeń jako jej pierwiastek.
| |
| − | | |
| − | [[Plik:Rozklad_poissona.png|300px|thumb|left|<figure id="fig:rozw2"></figure>Rozkłady Poissona dla różnych wartości parametru <math>\lambda</math>.]] | |
| − | | |
| − | ==Rozkład Gaussa==
| |
| − | | |
| − | Rozkład Gaussa (zwany też rozkładem normalnym lub krzywą dzwonową) zależy od
| |
| − | parametrów <math>\mu</math> i <math>\sigma</math>. Jego gęstość prawdopodobieństwa określona jest wzorem:
| |
| − | <equation id="eq:78">
| |
| − | <math>
| |
| − | p(x)=N(\mu, \sigma)= \frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-(x-\mu )^{2}}{2\sigma ^{2}}}.
| |
| | </math> | | </math> |
| | </equation> | | </equation> |
| | | | |
| − | Parametry te są tak dobrane, że wartość oczekiwana wynosi
| + | Dlaczego gęstość, a nie po prostu rozkład prawdopodobieństwa, jak w |
| − | <math>\mu</math>, a wariancja <math>\sigma^2</math>, co można
| + | przypadku dyskretnym? Właśnie ze względu na problemy z odczytem |
| − | sprawdzić wstawiając <xr id="eq:78">(%i)</xr> do wzorów na
| + | prawdopodobieństwa dla konkretnej wartości zmiennej. Na podobny |
| − | [[STAT:Momenty#label-eq:60|wartość oczekiwaną]] i
| + | problem trafiamy np. w fizyce, próbując obliczyć masę punktu. Masa to |
| − | [[STAT:Momenty#label-eq:63|wariancję]].
| + | iloczyn (całka) gęstości i objętości, a punkt ma zerową objętość. Aby |
| − | | + | otrzymać niezerową masę, gęstość materii musimy scałkować w jakimś |
| − | [[Plik:Rozklad_gaussa.png|300px|thumb|left|<figure
| + | niezerowym obszarze — nie można przyjąć za masę gęstości materii w |
| − | id="fig:rozklad_gaussa"></figure><math>N(0,1)</math>, czyli
| + | danym punkcie. Tak samo w przypadku ciągłych rozkładów gęstości |
| − | standardowy rozkład Gaussa o zerowej średniej (<math>\mu=0</math>) i
| + | prawdopodobieństwa, prawdopodobieństwo możemy obliczyć tylko dla |
| − | jednostkowej wariancji (<math>\sigma=1</math>).]]
| + | niezerowego przedziału zmiennej losowej, a wartość odczytywaną dla |
| − | | + | konkretnej wartości zmiennej losowej interpretujemy jako gęstość. |
| − | Rozkład Gaussa dla zerowej wartości oczekiwanej i jednostkowej
| |
| − | wariancji (<math>\mu=0, \sigma^2=1</math>) zwiemy ''standardowym
| |
| − | rozkładem Gaussa'' i oznaczamy zwykle <math>N(0,1)</math>.
| |
| − | Przedstawia go rysunek <xr id="fig:rozklad_gaussa"> %i</xr>.
| |
| − | Zaznaczono na nim m. in. wartość całki od <math>-\infty</math> do
| |
| − | <math>-1</math>, czyli prawdopodobieństwo, że wylosowana z tego
| |
| − | rozkładu liczba będzie mniejsza niż <math>-1</math>. Jak widać, wynosi
| |
| − | ono ok. 16%, a jeśli weźmiemy pod uwagę również wartości większe od 1,
| |
| − | będzie to aż 32%! Oznacza to, że przy losowaniu wielu liczb z tego
| |
| − | rozkładu prawie dwie spośród pięciu mogą znaleźć się w odległości
| |
| − | większej niż <math>\sigma</math> od wartości oczekiwanej. Warto o tym
| |
| − | pamiętać, gdyż odchylenie standardowe <math>\sigma</math> bywa czasami
| |
| − | nazywane "błędem". Stwierdzenie "w granicach błędu" może odnosić się
| |
| − | raczej np.do wartości 3<math>\sigma</math>: prawdopodobieństwo
| |
| − | wylosowania wartości oddalonej od średniej o więcej niż
| |
| − | <math>3\sigma</math> dla rozkładu Gaussa wynosi zaledwie 0,3 wartości
| |
| − | prawdopodobieństw odchyleń większych niż <math>1\div 3\sigma</math>
| |
| − | dla zmiennych z rozkładu normalnego:
| |
| − | | |
| − | <equation id="eq:80">
| |
| − | <math>
| |
| − | x\in N(\mu,\sigma)\quad \Rightarrow \quad
| |
| − | \begin{cases}
| |
| − | P(\left| x-\mu \right| \geq \sigma )\approx 0,\!317,\\
| |
| − | P(\left| x-\mu \right| \geq 2\sigma )\ \approx 0,\!046,\\
| |
| − | \ P(\left| x-\mu \right| \geq 3\sigma )\approx 0,\!003.
| |
| − | \end{cases}
| |
| − | </math>
| |
| − | </equation>
| |
| − | | |
| − | Należy jednak pamiętać, że gęstość prawdopodobieństwa dana równaniem
| |
| − | <xr id="eq:78">(%i)</xr> zanika w nieskończoności tylko
| |
| − | asymptotycznie, i dlatego w świetle tego rozkładu prawdopodobieństwo
| |
| − | wylosowania ''dowolnej'' wartości będzie niezerowe (choć dla
| |
| − | większości niezmiernie małe). Prowadzi to czasem do paradoksów, jak
| |
| − | np. niezerowe prawdopodobieństwo ujemnej masy.<ref>Gaussowski
| |
| − | rozkład pomiarów jakiejkolwiek masy, określony dodatnimi wartościami
| |
| − | <math>\mu</math> i <math>\sigma</math>, będzie wykazywał nieujemne —
| |
| − | choć zapewne bardzo małe — prawdopodobieństwo również dla ujemnych
| |
| − | wartości zmiennej losowej, którą w tym przypadku będzie mierzona | |
| − | masa.</ref> Jest to cena za korzystanie ze zwięzłej i eleganckiej
| |
| − | postaci analitycznej rozkładu.
| |
| − | | |
| − | --------------------
| |
| − | <references>
| |
Wnioskowanie_Statystyczne_-_wykład
Rozkłady prawdopodobieństwa
Rozkład prawdpopodobieństwa — zgodnie z nazwą — będzie funkcją określającą,
jak prawdopodobieństwo rozkłada się pomiędzy możliwe wyniki danego
doświadczenia. Mieliśmy już z nim do czynienia w pierwszej części książki,
rysunek 1 przypomina niektóre z tych przypadków.
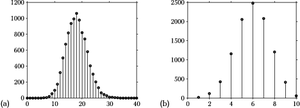
(a) rozkład liczby jedynek uzyskany z 10 tysięcy repróbkowań ze zwracaniem (bootstrap) próby 18 jedynek i 82 zer; (b) liczba trafień na 10 rzutów do kosza, przy średnim prawdopodobieństwie trafienia 0,6
Nie są to prawdopodobieństwa, gdyż nie spełniają aksjomatu [math](0\leq P(A)\leq 1)[/math], który wraz z aksjomatem [math](P(\Omega)=1)[/math] możemy spełnić dzieląc liczbę wystąpień każdego przypadku przez całkowitą liczbę eksperymentów —
wtedy suma wszystkich prawdopodobieństw (czyli [math]P(\Omega)[/math])
wyniesie 1. Przykład tak znormalizowanego dyskretnego rozkładu
prawdopodobieństwa przedstawia rysunek rysunek 2(a).
Pozostaje jeszcze problem formalny: występujące w klasycznej teorii
funkcje nie są określone na zdarzeniach, tylko na liczbach. Przejście
od zdarzeń do odpowiadających im liczb wymaga pojęcia zmiennej
losowej – odwzorowania [math]X(.)[/math] z przestrzeni zdarzeń do
przestrzeni liczb rzeczywistych. Na przykład w doświadczeniu
polegającym na rzucaniu kostką zmienna losowa przypisze liczbę 4
przypadkowi, w którym na górnej ściance rzuconej kostki widać cztery
kropki.
Liczby (czyli zmienne losowe) są już pełnoprawnymi argumentami
funkcji, ale z definicją rozkładu prawdopodobieństwa będzie jeszcze
trochę kłopotu, jeśli wyniki eksperymentu będą pochodzić z ciągłych
przedziałów zmiennej losowej, a nie, jak w przykładach z rysunku rysunek 1, ze zbioru dyskretnego.
Rozkłady ciągłe — gęstość prawdopodobieństwa
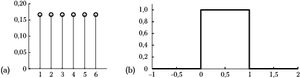
(a) dyskretny rozkład prawdopodobieństw wyników rzutu kostką; (b) ciągły rozkład prawdopodobieństwa dla liczb rzeczywistych z przedziału od zera do jednego.
Z rozkładem ciągłym mieliśmy do czynienia, gdy używaliśmy generatora
liczb losowych — losował on z równym prawdopodobieństwem liczby
rzeczywiste z przedziału od zera do jednego. Funkcja przypisująca
równe prawdopodobieństwa liczbom od zera do jednego powinna wyglądać
jak na rysunku 2(b). A jednak coś się
tu nie zgadza...
Zacznijmy od rozkładu dyskretnego, czyli wykresu 2(a). Prawdopodobieństwo dla
zmiennej losowej (teraz nie jest to już formalnie zdarzenie)
wynoszącej na przykład 2 odczytujemy jako wynoszące 0,167. Czyli
mniejsze od 1 i większe od zera. Suma prawdopodobieństw dla wszystkich
możliwych wartości zmiennej losowej wyniesie 1 — wszystko zgadza się
z aksjomatami definicji prawdopodobieństwa.
Teraz spróbujmy z wykresu po prawej stronie odczytać wartość
prawdopodobieństwa wylosowania jakiejś liczby spomiędzy 0 i 1. Jeden?
To oznacza pewność — niemożliwe. Na osi [math]y[/math] powinna
występować jakaś znacznie mniejsza wartość... Ale jaka?
Zastanówmy się: niezależnie od tego, jak małą (niezerową i nieujemną)
wartość przyjmiemy dla prawdopodobieństwa wylosowania dowolnej liczby
z tego przedziału, to gdy zaczniemy je sumować dla wszystkich
możliwych wyników, których na odcinku [math](0, 1)[/math] jest wszak
nieskończenie wiele, zawsze dostaniemy więcej niż jeden. Najwyraźniej
tak się nie da.
Widać już, że sumę będziemy musieli zastąpić całką — jest to właśnie
graniczny przypadek sumy. W tym układzie aksjomat
[math]P(\Omega)=1[/math], który dla przypadku dyskretnego wyrażał się
sumą
[math]
\sum_i P(X=x_i) = 1,
[/math]
teraz będzie wyrażał się całką
[math]
\int p(x) dx = 1,
[/math]
gdzie prawdopodobieństwo [math]P[/math] zastąpiła, z przyczyn, które
staną się jasne za chwilę, gęstość prawdopodobieństwa [math]p[/math].
Łatwo sprawdzić, że całka rozkładu z rys. 2 spełnia ten warunek. Jednak
pozostaje problem odczytywania wartości prawdopodobieństwa dla
konkretnej wartości zmiennej losowej.
Przypomnijmy sobie, że symulując rzuty monetą korzystaliśmy z faktu, że prawdopodobieństwo wylosowania liczby
mniejszej niż [math]\frac1 2[/math] wynosi 0,5. Zdefiniujmy więc
dystrybuantę prawdopodobieństwa zmiennej losowej [math]X[/math]
jako prawdopodobieństwo wystąpienia któregokolwiek ze zdarzeń, dla
których zmienna losowa przyjmuje wartości mniejsze od [math]x[/math]:
[math]
F(x)=P[X \leq x].
[/math]
Będzie to oczywiście funkcja niemalejąca, dążąca do zera dla małych
[math]x[/math] i do jednego dla dużych. Dla rozkładu z rysunku 2(b) dystrybuanta będzie wyglądać
jak na rysunku 3.
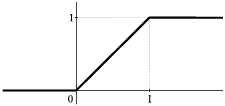
Dystrybuanta ciągłej zmiennej losowej o równym prawdopodobieństwie na przedziale (0, 1).
Dopiero teraz gęstość prawdopodobieństwa zmiennej losowej określimy jako
pochodną dystrybuanty
[math]
p(x)=\frac{d F(x)}{dx}=\frac{P[x\leq X\leq x+dx]}{dx}.
[/math]
Dlaczego gęstość, a nie po prostu rozkład prawdopodobieństwa, jak w
przypadku dyskretnym? Właśnie ze względu na problemy z odczytem
prawdopodobieństwa dla konkretnej wartości zmiennej. Na podobny
problem trafiamy np. w fizyce, próbując obliczyć masę punktu. Masa to
iloczyn (całka) gęstości i objętości, a punkt ma zerową objętość. Aby
otrzymać niezerową masę, gęstość materii musimy scałkować w jakimś
niezerowym obszarze — nie można przyjąć za masę gęstości materii w
danym punkcie. Tak samo w przypadku ciągłych rozkładów gęstości
prawdopodobieństwa, prawdopodobieństwo możemy obliczyć tylko dla
niezerowego przedziału zmiennej losowej, a wartość odczytywaną dla
konkretnej wartości zmiennej losowej interpretujemy jako gęstość.



