Funkcja systemu
Spis treści
AS/ Transformata Z i widmo procesu AR
Transformata Z
Jednostronna transformata [math]\mathcal{Z}[/math] ciągu liczb [math]x[n][/math] definiowana jest jako funkcja zmiennej [math]z[/math] będąca sumą szeregu
- [math] \displaystyle \mathcal{Z}\{x[n]\} = X(z)= \sum_{n=0}^{\infty} x[n] z^{-n} [/math]
czyli np. [math] \mathcal{Z}\{(2, 7, 3)\} = 2 z + 7 z^{-1} + 3 z^{-2} [/math]
Dla [math]z=e^{i \omega}[/math] dostajemy Dyskretną Transformatę Fouriera.
- [math] \displaystyle X(z=e^{i \omega})= \sum_{n=0}^{\infty} x[n] e^{- i \omega n} [/math]
Transformata [math]\mathcal{Z}[/math] jest liniowa
- [math] \displaystyle \mathcal{Z}\lbrace a x[n] + b y[n]\rbrace =a X[z] + b Y[z] [/math]
a dla przesunięcia w czasie
- [math] \displaystyle \mathcal{Z}\lbrace x[n-k]\rbrace = z^{-k}X(z) [/math]
Dowód:
- [math] \displaystyle \mathcal{Z}\lbrace x[n-k]\rbrace = \sum_{n=0}^{\infty} x[n-k] z^{-n} \;\; \stackrel{ j \rightarrow n-k }{=} \;\; \sum_{j=-k}^{\infty} x[j] z^{-(j+k)} = [/math]
- [math] \displaystyle = \sum_{j=-k}^{\infty} x[j] z^{-j} z^{-k} = z^{-k} \sum_{j=-k}^{\infty} x[j] z^{-j} [/math]
dla systemów przyczynowych [math]x[j][/math] są niezerowe dla [math]j\gt 0[/math] (por. LTI/Splot i przyczynowość)
więc
- [math]\displaystyle \mathcal{Z}\lbrace x[n-k]\rbrace = z^{-k} \sum_{j=0}^{\infty} x[j] z^{-j} [/math]
Niech [math]x[n]=x_1[n]*x_2[n][/math]; wtedy transformata [math]\mathcal{Z}[/math] splotu to iloczyn transformat [math]\mathcal{Z}[/math]:
- [math] \displaystyle \mathcal{Z}\{x[n]\} = X(z) = \mathcal{Z}\{x_1[n]\} \mathcal{Z}\{x_2[n]\} = X_1(z) X_2(z) [/math]
Dowód:
- [math] \displaystyle \mathcal{Z}\{x_1(n)*x_2(n)\} = X(z) = [/math]
- [math] \displaystyle \sum_{n=-\infty}^\infty\left[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)\right]z^{-n}[/math]
- [math]= \displaystyle \sum_{k = -\infty}^\infty x_1(k)\left[\sum_{n=-\infty}^\infty x_2(n-k)z^{-n}\right][/math]
- [math]= \displaystyle \sum_{k = -\infty}^\infty x_1(k)\left[\sum_{n = -\infty}^\infty x_2(n-k)z^{-(n-k)}z^{-k}\right] [/math]
- niech [math]n-k = l[/math]
- [math] \displaystyle X(z) = \sum_{k = -\infty}^\infty x_1(k)\left[z^{-k}\sum_{l=-\infty}^\infty x_2(l)z^{-l}\right][/math]
- [math]= \displaystyle \sum_{k = -\infty}^\infty x_1(k) z^{-k} X_2(z)[/math]
- [math]= \displaystyle X_1(z) X_2(z) [/math]
Widmo procesu AR
kładąc [math] a_0 = 1[/math], proces AR o znanych współczynnikach [math]a_i[/math]
- [math] \displaystyle x[n] = \sum_{i=1}^M a_i x[n-i] + \epsilon[n] [/math]
możemy zapisać jako
- [math] \displaystyle \sum_{i=0}^M a_i x[n-i] = \epsilon[n] [/math]
Biorąc transformatę Z obu stron
- [math] \displaystyle \mathcal{Z}\left\{\sum_{i=0}^M a_i x[n-i] \right\} = \mathcal{Z}\left\{ \epsilon[n] \right\} [/math]
dostajemy
[math] A(z) X(z) = E(z) [/math]
[math] X(z) = \dfrac{E(z)}{A(z)} [/math]
oznaczając
[math]\displaystyle H(z) \stackrel{def}{=} A^{-1}(z) = \dfrac{1}{\sum a_i z^{-i}}[/math]
dostajemy
[math] X(z) = H(z) E(z) = \dfrac{E(z)}{a_0 + a_1 z^{-1} + a_2 z^{-2} + \ldots} [/math]
podstawiając [math]z=e^{i\omega t}[/math] przechodzimy z transformaty [math]\mathcal{Z}[/math] do transformaty Fouriera [math]\mathcal{F}(x) = \hat{x}(\omega)[/math]
- [math] \hat{x}(\omega) = H(\omega) E(\omega) [/math]
widmo to kwadrat modułu transformaty Fouriera
- [math] \displaystyle \left| \hat{x}(\omega) \right| ^2 = \left| H(\omega) E(\omega) \right|^2 = \\ \,\;\;\;\;\;\;\;\;\;\; = \left| H(\omega) \right|^2 \sigma^2 = \dfrac{\sigma^2}{\left| {A(e^{-i\omega n})} \right|^2} = \dfrac{\sigma^2}{\left|a_0 + a_1 e^{-i\omega} + a_2 e^{- 2 i\omega} + \ldots \right|^2} [/math]
gdzie [math]\sigma^2[/math] to wariancja nieskorelowanego szumu [math]\epsilon[/math], którego widmo jest płaskie (nie zależy od częstości)
Wielozmienny model AR
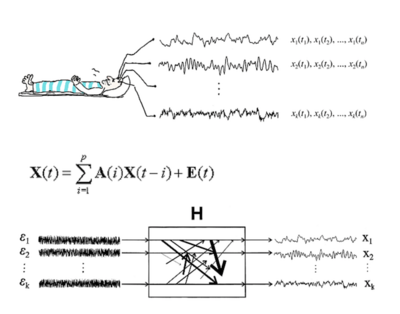
Model AR opisuje wartość sygnału w chwili [math]t[/math] jako kombinację liniową jego wartości w chwilach poprzednich (oraz szumu). W przypadku wielowymiarowym możemy włączyć do tego opisu wartości wszystkich sygnałów [math]s_i[/math], czyli wektora [math]\vec{s}(t)[/math]. Wielozmienny model AR (MVAR, multivariate autoregressive) można wówczas opisać wzorem:
[math]
\displaystyle
\vec{s}(t)=\sum_{i=1}^p A(i) \vec{s}(t-i) + \vec{\epsilon}(t) ,
[/math]
gdzie [math]\vec{\epsilon}(t)[/math] będzie wektorem
szumów, zaś [math]A(i)[/math] będą macierzami współczynników modelu.
Przechodząc do przestrzeni częstości otrzymamy:
[math]
\displaystyle
\vec{s}(\omega)=A^{-1}(\omega)\vec{\epsilon}(\omega)=H(\omega)\vec{\epsilon}(\omega),
[/math]
gdzie [math]H(\omega)[/math] jest macierzą przejścia. MVAR jest modelem typu "czarna skrzynka", gdzie na wejściu występują szumy, na wyjściu sygnały, a system jest opisany przez macierz przejścia. Zawiera ona informacje o własnościach widmowych sygnałów i związkach między nimi.
Na podstawie macierzy [math]H(\omega)[/math] można obliczyć macierz
gęstości widmowej zawierającą widma mocy dla pojedynczych kanałów jak
również funkcje wzajemnej gęstości mocy pomiędzy kanałami. Stosując
tego typu podejście, w którym wszystkie sygnały generowane przez
pewien proces są rozpatrywane jednocześnie, można policzyć z macierzy
spektralnej nie tylko koherencje zwykłe pomiędzy dwoma kanałami, ale
również koherencje wielorakie opisujące związek danego kanału z
pozostałymi i koherencje cząstkowe opisujące bezpośrednie związki
między dwoma kanałami po usunięciu wpływu pozostałych kanałów. W
przypadku gdy pewien kanał 1 będzie wpływał na kanały 2 i 3,
obliczając koherencję zwykłą znajdziemy związek między 2 oraz 3,
chociaż nie są one ze sobą bezpośrednio powiązane, natomiast
koherencja cząstkowa nie wykaże związku między nimi.
Macierz [math]H(\omega)[/math] jest niesymetryczna, a jej wyrazy
pozadiagonalne mają sens przyczynowości Grangera, co oznacza, że
uwzględnienie wcześniejszej informacji zawartej w jednym z sygnałów
zmniejsza błąd predykcji drugiego sygnału. Opierając się na tej
własności zdefiniowano Kierunkową Funkcję Przejścia (DTF, directed
transfer function) jako znormalizowany element pozadiagonalny
[math]H(\omega)[/math]. DTF opisuje kierunek propagacji i skład
widmowy rozchodzących się sygnałów.
Otrzymamy w ten sposób całościowy opis zmian wszystkich sygnałów
jednocześnie. Co ciekawe, obliczona na tej podstawie funkcja
charakteryzująca zależności między sygnałami [math]s_i[/math] (funkcja
przejścia) nie jest symetryczna, w przeciwieństwie do
np. korelacji. Dzięki temu może służyć wnioskowaniu nie tylko o sile
zależności między poszczególnymi sygnałami składowymi, ale też o
kierunku przepływu informacji między nimi. W przybliżeniu odpowiada
to informacji, w którym z sygnałów struktury odpowiadające danej
częstości pojawiają się wcześniej.